USING C++ LANGUAGE ONLY. PLEASE USE knowledge BELOW AND FOLLOW THE OUTPUT EXAMPLE GIVEN.

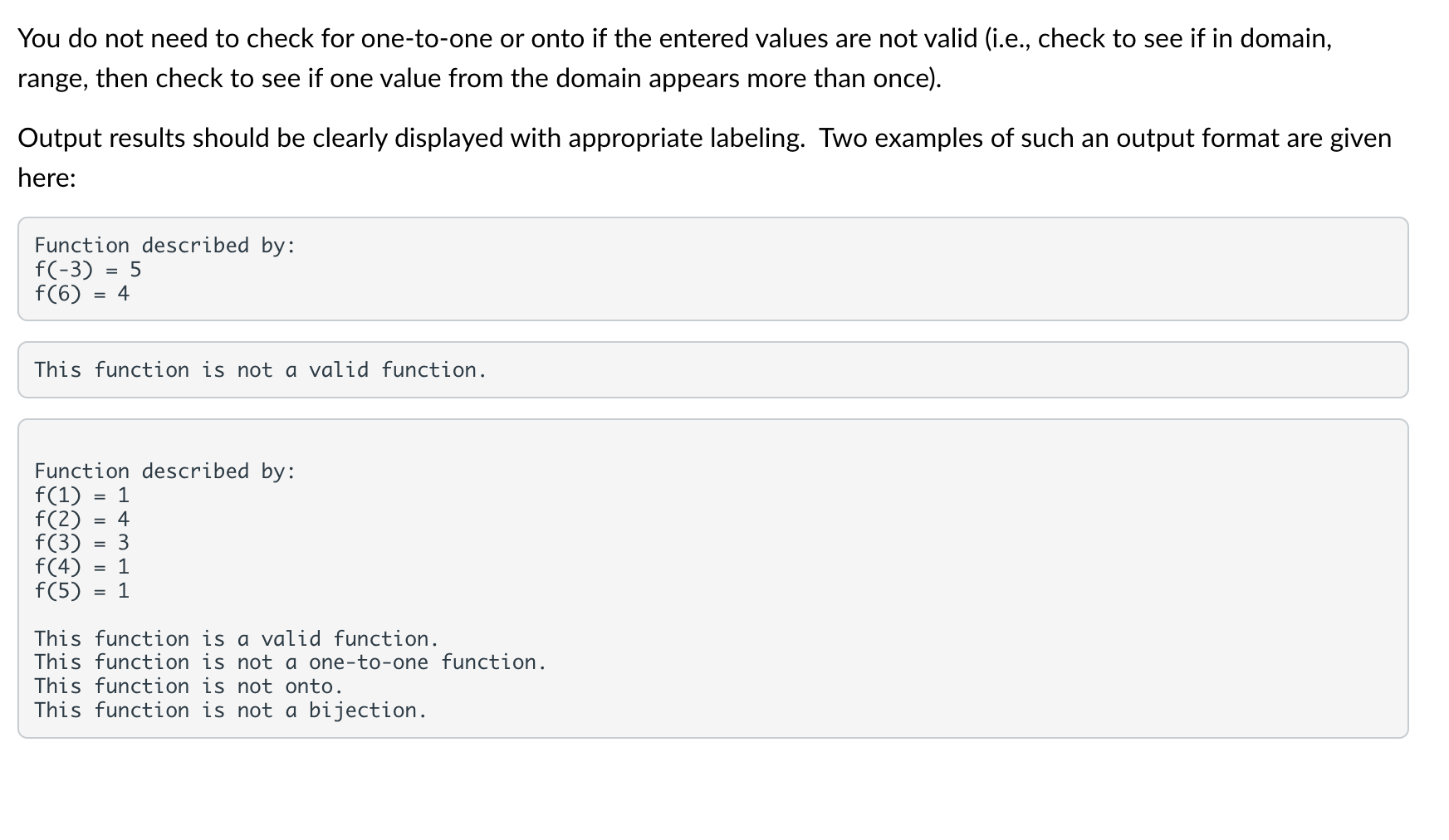
Given a function f from A={1,2,3,4,5} to itself, write a C,C++ or Java program to determine whether f is a valid function, one-to-one, onto, and/or a bijection. Valid function: no x value has two y values and all x and y values are part of the Domain and Range respectively (we will accept partial functions as valid) One-to-one: No y value has more than one x that maps to it (e.g., f(3)=2 and f(4)=2 is NOT one-to-one) Onto: for every y in the Range, there is at least one x such that f(x)=y. Bijection: the function is both one-to-one and onto Input should be entered through console prompts. Here is a sample program for this part: This is a command line program that can be run in Windows. Your program should ask for the number of ordered pairs, then read each pair as one line of input. Do NOT use strings for your input unless you use it only to perform error checking before converting the read values to integers. If the values entered are not in the Domain or Range, keep reading in the ordered pairs, do not abort if a domain or range value is wrong. Functions can be described as a set of ordered pairs. The program will be tested with the following sets of ordered pairs, written in F(x)=y form, though you should only look for xy on each input line: You do not need to check for one-to-one or onto if the entered values are not valid (i.e., check to see if in domain, range, then check to see if one value from the domain appears more than once). Output results should be clearly displayed with appropriate labeling. Two examples of such an output format are given here: Function described by: f(3)=5f(6)=4 This function is not a valid function. Function described by: f(1)=1 f(2)=4 f(3)=3 f(4)=1 f(5)=1 This function is a valid function. This function is not a one-to-one function. This function is not onto. This function is not a bijection