Using C++, python or Matlab

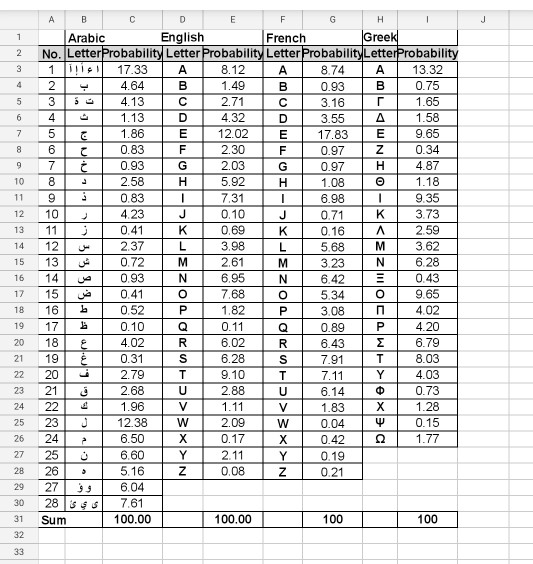
Given a language with letter alphabet , of size n = ||, the entropy of the letters is Hu = log n if all letters of the alphabet are equally probable. In actual use of the language, this might not be the case and the computed entropy Hexp from texts of the language would be different from Hu. The letter redundancy of the language may be taken as R = 1- Hexp / Hu. This means that only (1 R)n letters can be used effectively to write most of the language texts. The file Letter Frequency.xlsx gives the letter frequencies observed for four different languages (Arabic, English, French and Greek). Given these frequencies, compare the redundancies of the given four languages.

Using python language

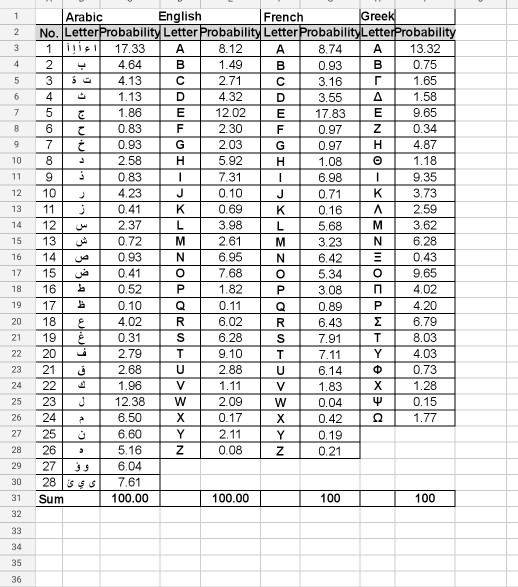
2 4 . 1.13 E F 3.73 Arabic English French Greek No. Letter Probability Letter Probability Letter Probability LetterProbability 1 17.33 A 8.12 A 8.74 A 13.32 4.64 B 11.49 B 10.93 B 0.75 4.13 C 2.71 C 3.16 r. 1.65 D 4.32 D 1.58 1.86 12.02 9.65 0.83 2.30 F Z 0.34 0.93 2.03 G H 4.87 2.58 H 5.92 1.18 0.83 7.31 9.35 4.23 0.10 0.41 0.69 2.59 237 3.98 3.62 0.72 2.61 6.28 0.93 N 6.95 0.43 0.41 o 7.68 9.65 0.52 1.82 4.02 0.10 0.11 4.20 4.02 6.02 6.79 19 0.31 6.28 7.91 8.03 2.79 9.10 7.11 Y 4.03 2.68 U 2.88 6.14 0.73 1.96 1.11 1.83 1.28 12.38 w 2.09 0.04 0.15 6.50 0.17 X 0.42 1.77 6.60 2.11 Y 0.19 5.16 Z 0.08 Z 0.21 6.04 $$ 7.61 Sum 100.00 100.00 100 100 MH33 334 L M Q W 21 7.58 0.83 w Arabic English French Greek No. Letter Probability Letter Probability Letter Probability Letter Probability 1 Title 17.33 8.12 A 8.74 13.32 4 64 149 0.93 B 0.75 35 4 13 3.16 1.65 1 13 3.55 17.83 0.97 71 093 0.97 4 87 10 8 a 259 5.92 1.08 1.18 119 083 7.31 6.98 9.35 12 10 4.23 0 10 0.71 3.73 13 11 0.41 0.69 0.16 259 14 12 2.37 3.98 5.68 3.62 15 13 0.72 2.61 M 3.23 N 6.28 16 14 | 0.93 6.95 N 6.42 0.43 17 15 0.41 7.68 5.34 9.65 18 16b 0.52 1.82 3.08 4.02 1917 0.10 0.11 0.89 4.20 2018 4.02 R 6.02 6.43 6.79 2119 0.31 6.28 7.91 8.03 2.79 T 9.10 7.11 Y 4.03 2.68 2.88 6.14 0.73 1.96 1.11 V 1.83 X 1.28 12.38 2.09 W 0.04 V 0.15 6.50 0.17 0.42 1.77 27 253 6.60 Y 0.19 28 26 5.16 TZ 0.08 Z1 0.21 2927 ) 6.04 30 28 S S $ 7.61 Sum 100.00 100.00 100 N alalalalala Y 100 Given a language with letter alphabet , of size n = ), the entropy of the letters is H. = logn if all letters of the alphabet are equally probable. In actual use of the language, this might not be the case and the computed entropy Hep from texts of the language would be different from H. The letter redundancy of the language may be taken as R = 1. Hy/H.. This means that only (1-R)n I letters can be used effectively to write most of the language texts. The file 'Letter Frequency.xlsx' gives the letter frequencies observed for four different languages (Arabic, English, French and Greek). Given these frequencies, compare the redundancies of the given four languages