Using dr-racket

Redesign find-path/list so that it uses an existing list abstraction from figures 95 and 96 instead of explicit structural recursion. Hint Read the documentation for Rackets ormap. How does it differ from ISL+s ormap function? Would the former be helpful here?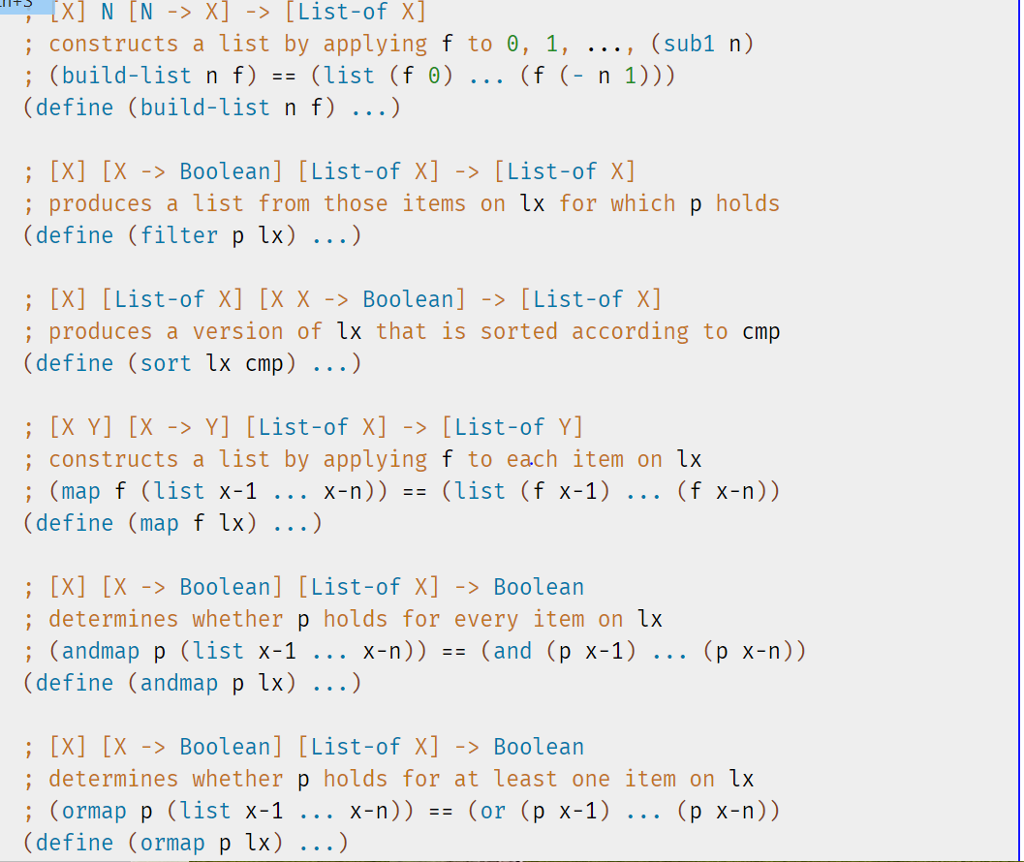

XN[N ->X] -> [List-of X ; constructs a list by applying f to , 1, , (sub1 n) ; (build-list n f) -- (list (f ) (f (-n 1))) (define (build-list nf) ...) [X] [X -Boolean] [List-of X]List-of X] ; produces a list from those items on for which p holds (define (filter p lx) ...) ; [X] [List-of X] [X X -Boolean] - [List-of X] ; produces a version of lx that is sorted according to cmp (define (sort lx cmp) ...) ; [X Y] [X - Y] [List-of X]- [List-of Y] ; constructs a list by applying f to each item on lx ; (map f (list x-1 x-n)) -- (list (f x-1) (f x-n)) (define (map f ) ) ; [X] [X-Boolean] [List-of X]-Boolean ; determines whether p holds for every item on lx ; (andmap p (list x-1 X-n))(and (p x-1) (define (andmap p ) ) ; [X] [X-Boolean] [List-of X]Boolean ; determines whether p holds for at least one item on lx ; (ormap p (list x-1 x-n)) -(or (p x-1) (p x-n)) (define (ormap p ) ) XN[N ->X] -> [List-of X ; constructs a list by applying f to , 1, , (sub1 n) ; (build-list n f) -- (list (f ) (f (-n 1))) (define (build-list nf) ...) [X] [X -Boolean] [List-of X]List-of X] ; produces a list from those items on for which p holds (define (filter p lx) ...) ; [X] [List-of X] [X X -Boolean] - [List-of X] ; produces a version of lx that is sorted according to cmp (define (sort lx cmp) ...) ; [X Y] [X - Y] [List-of X]- [List-of Y] ; constructs a list by applying f to each item on lx ; (map f (list x-1 x-n)) -- (list (f x-1) (f x-n)) (define (map f ) ) ; [X] [X-Boolean] [List-of X]-Boolean ; determines whether p holds for every item on lx ; (andmap p (list x-1 X-n))(and (p x-1) (define (andmap p ) ) ; [X] [X-Boolean] [List-of X]Boolean ; determines whether p holds for at least one item on lx ; (ormap p (list x-1 x-n)) -(or (p x-1) (p x-n)) (define (ormap p ) )