Question: Using equations (15.4) and (15.5), show that Jo(x) = J2(x) at every maximum or %3D minimum of Ji(x), and Jo(r) = -J2(x) Computer plot

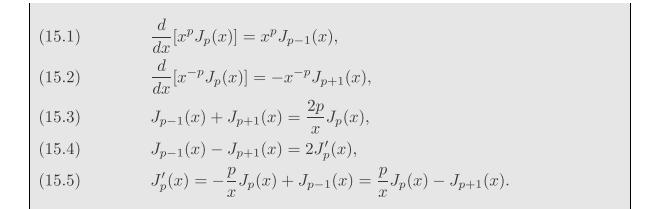
Using equations (15.4) and (15.5), show that Jo(x) = J2(x) at every maximum or %3D minimum of Ji(x), and Jo(r) = -J2(x) Computer plot

Using equations (15.4) and (15.5), show that Jo(x) = J2(x) at every maximum or %3D minimum of Ji(x), and Jo(r) = -J2(x) Computer plot Jo(x), Ji(x), and J2(a) on the same axes, and verify that these J{ (x) at every positive zero of J(x). results are true. (15.1) la" J,(r)] = r" Jp-1(x), dr d. [rPJp(x)] = --PJp+1(x), (15.2) dr Jp-1(x) + Jp+1(x) = "J,(x), Jp-1(x) Jp+1(a) = 2., (a), J,(x) = -J,(x) + Jp-1(r) = Jp(x) Jp+1(x). (15.3) (15.4) (15.5)

Step by Step Solution

★★★★★

3.49 Rating (172 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve the given problem we need to verify the relationships between Bessel functions J0x J1x and ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Physics Questions!

Using equations (15.4) and (15.5), show that Jo(r) = J2(r) at every maximum or minimum of Ja (x), and Jo(r) Computer plot Jo(x), Ji(x), and J2(a) on the same axes, and verify that these results are...

3 / 4 1 1 / 4 x

Using (2), show that for every x , e-x = 1/ex ex > 0 ex as x and ex 0 as x - This implies that the exponential function maps onto +.

Write a memo on Determining Audience Needs. In a memo to your communications team, instruct them on ways to discover the needs of the stakeholders in different areas of the company so that a new...

Write an article on Data Processing and Management System Korle-Bu Teaching Hospital is the third largest hospital in Africa and the leading national referral center in Ghana. It was established as a...

Use the following data of Starfish Sales, Inc.: Unit Total Units Units Cost Cost Sold Beginning inventory 18 $5 $90 Purchase on Apr 25 37 8 296 Purchase on Nov 16 20 9 180 Sales 45 ? ? Starfish Sales...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Census in India is being held regularly after every a) 6 years b) 8 years c) 10 years d) 12 years

The adjusted trial balance columns of the worksheet for Savaglia Company are as follows. Instructions Complete theworksheet. SAVAGLIA COMPANY Worksheet (partial) For the Month Ended April 30, 2017...

11.01-PR001 Uncertainty can impact many elements of an engineering economic analysis. Given the list of factors below, rank them from most to least uncertain and briefly justify why you ranked them...

HEIJUNKA SCHEDULING OF CUSTOMERS' ORDERS The production manager at a factory manufacturing four types of light fittings (A, B, C and D) on an automated machine is fixing the schedule for the next...

A car with load q is parked at the left side of a steel bridge, while a truck with load ris parked at the right side. Without special programs (Excel and calculator are fine), find the maximum...

Sun Inc. is contemplating a tender offer to acquire 80% of Moon Corporation's common stock. Moon's shares are currently quoted on the New York Stock Exchange at $25 per share In order to have a...

A farmer has an acre of specialty vegetables and is preparing for the summer harvest. Historically, this acre has yielded an average of 2,100 lbs of product with a standard deviation of 950 lbs. A...

Case study: (50 marks) -PART A On 1 July 2021, Tom Ltd acquired all the shares of Hanks Ltd on an ex-div . basis. Tom Ltd paid $850,000 cash and issued 120,000 shares which had a fair value of $5.00...

Which two amendments to the Constitution include a due process clause? Group of answer choices 1st and 5th 5th and 8th 2nd and 8th 5th and 14th 14th and 10th

(15.1) la" J,(r)] = r" Jp-1(x), dr d. [rPJp(x)] = --PJp+1(x), (15.2) dr Jp-1(x) + Jp+1(x) = "J,(x), Jp-1(x) Jp+1(a) = 2., (a), J,(x) = -J,(x) + Jp-1(r) = Jp(x) Jp+1(x). (15.3) (15.4) (15.5)

6. Using Tables 15-4 and 15-5, convert the following assembly language to machine code. LOADA 100016 LOADB 100116 JGT AGREATER EXCAB AGREATER: STORA 100216 01 M 04 OS Machine code Assembly language...

10. Using Tables 15-4 and 15-5, convert the following machine code to assembly language starting at address 200016 Address Data 20001602 20011613 2002164E 20031605 20041613 2005164F 20061608 20071605...

Part 1 (25 points) Using exhibit 2.1 (US treasury rates) assume that the maturity date is exactly 2 or 3 years from now (chapter 12, result 12.4 has the formula for cost of carry - we want to find...

Using exhibit 2.1 (US treasury rates) assume that the maturity date is exactly 2 or 3 years from now (chapter 12, result 12.4 has the formula for cost of carry we want to find the costs associated...

Please see the attached instructions forwhat is required for this question For this assignment, you will complete the Financial Overview component of Amazon. To complete this assignment, use the...