Question: Using Euler's equations in Cartesian form, or otherwise, show that under gravitational force alone the free surface of a fluid in solid body rotation with
Using Euler's equations in Cartesian form, or otherwise, show that under gravitational force alone the free surface of a fluid in solid body rotation with
yhatxhat
and hat vertically upwards, is a paraboloid.
A deep cylindrical bucket whose axis is vertical is of radius a and contains a layer of water initially at rest and of constant depth The bucket is rotated about its axis at angular velocity until the fluid is in solid body rotation. For what value of is precisely half the area of the bottom of the bucket dry?
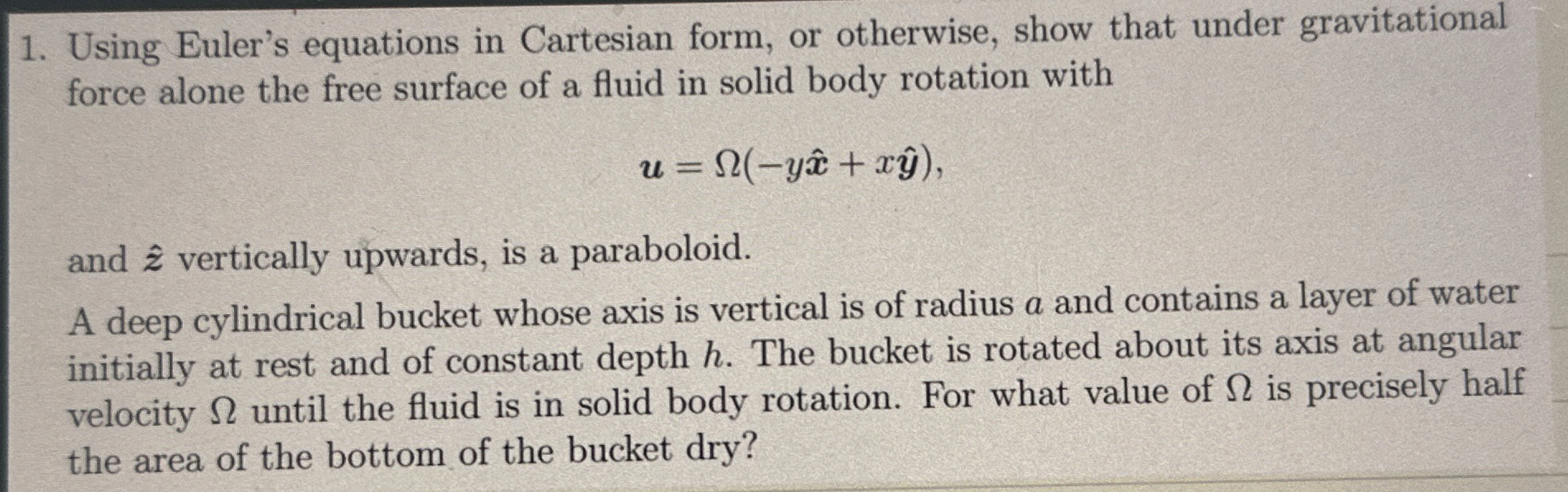
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


