Using Example 4.26 as your guide, find the Gauss-Newton procedure for estimating the autoregressive parameter,

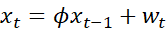
Example 4.26. GaussNewton for an MAO) Consider an MAO) process, :6; = w; + 9wt_1. Write the errors as wt(9) = x: Huh1(9), t = 1, . . . , n, (423} where we condition on we (6) = 0. Our goal is to nd the value of 6' that minimizes 5.:(9) = [211:1 10%(9), which is a nonlinear function of 0. Let 6(0) be an initial estimate of 6, for example the method of moments estimate. Now we use a rst-order Taylor approximation of wt(9) at 9(0) to get 3cm) = Zw) \" E[wt(6(l])) (9 9(0))Zt(9(0))]2~ (424) i=1 t=1 where a (9) 249(0)) = wt , 39 9:3(0) (writing the derivative in the negative simplies the algebra at the end). It turns out that the derivatives have a simple form that makes them easy to evaluate. Taking derivatives in (4.23), awda) _ aw _ 6 36 _ w,_1(9) _ 94g 89' t: 1,...,n, (4.25) where we set awe (9) /39 = 0. We can also write (4.25) as zt(9) = wt_1(6) Hzt_1(9), t = 1,. . . ,n, (4.26) where 20(9) = 0. This implies that the derivative sequence is an AR process, which we may easily compute recursively given a value of 9. We will write the right side of (4.24) as n 2 (2(9) = Z wt(9(0)) (9 9(0)) Zt(9(0))| (427) 1'2] T y: 2: and this is the quantity that we will minimize. The problem is now simple linear regression (\"yt = [32; + Q\"), so that (9 9(0)) = 3:1 Zt(9(0))wt(9(0)) / 2L1 2%(9(0))a or 9 = 9(0) + 2L1 Zt(9(o))wt(9(o)) / >321 09m)- Consequently, the GaussNewton procedure in this case is, on iteration j + 1, set 2L1 Zt(9(j))wt(9(j)) 6- =9-+, '=0,1,2,..., (4.28) (1+1) U) 11:1 z2090.\" where the values in (4.28) are calculated recursively using (4.23) and (4.26). The calculations are stopped when |9(j+1) 9U) I, or |Q(9(j+1)) me) , are smaller than some preset amount. \f\f\f