using excel VBA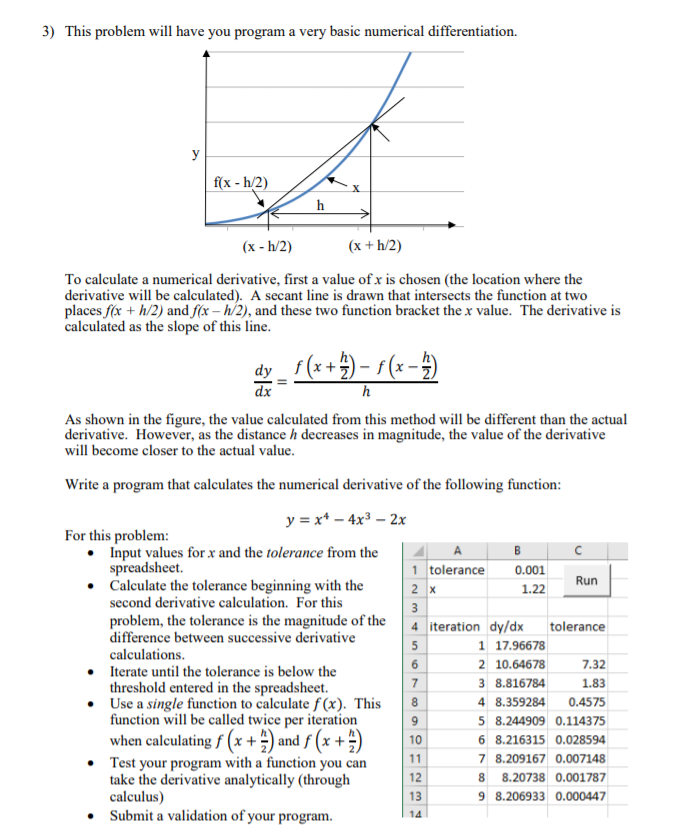
3) This problem will have you program a very basic numerical differentiation. f(x -h/2) (x -h/2) (x +h/2) To calculate a numerical derivative, first a value of x is chosen (the location where the derivative will be calculated). A secant line is drawn that intersects the function at two places for +h/2) and fx - h/2), and these two function bracket the x value. The derivative is calculated as the slope of this line dx As shown in the figure, the value calculated from this method will be different than the actual derivative. However, as the distance h decreases in magnitude, the value of the derivative will become closer to the actual value Write a program that calculates the numerical derivative of the following function y=x4-4x3-2x For this problem: Input values for x and the tolerance from the A spreadsheet. 1 tolerance0.001 1.22 Run . Calculate the tolerance beginning with the second derivative calculation. For this problem, the tolerance is the magnitude of the difference between successive derivative calculations. Iterate until the tolerance is below the threshold entered in the spreadsheet. .Use a single function to calculate f(x). This 8 function will be called twice per iteration iteration dy/dx tolerance 117.96678 10.64678 3 8.816784 7.32 1.83 4 8.359284 0.4575 8.244909 0.114375 6 8.216315 0.028594 8.209167 0.007148 8 8.20738 0.001787 9 8.206933 0.000447 when calculating f (x + ) and f (x + 110. .Test your program with a function you can take the derivative analytically (through calculus) 12 13 14 .Submit a validation of your program. 3) This problem will have you program a very basic numerical differentiation. f(x -h/2) (x -h/2) (x +h/2) To calculate a numerical derivative, first a value of x is chosen (the location where the derivative will be calculated). A secant line is drawn that intersects the function at two places for +h/2) and fx - h/2), and these two function bracket the x value. The derivative is calculated as the slope of this line dx As shown in the figure, the value calculated from this method will be different than the actual derivative. However, as the distance h decreases in magnitude, the value of the derivative will become closer to the actual value Write a program that calculates the numerical derivative of the following function y=x4-4x3-2x For this problem: Input values for x and the tolerance from the A spreadsheet. 1 tolerance0.001 1.22 Run . Calculate the tolerance beginning with the second derivative calculation. For this problem, the tolerance is the magnitude of the difference between successive derivative calculations. Iterate until the tolerance is below the threshold entered in the spreadsheet. .Use a single function to calculate f(x). This 8 function will be called twice per iteration iteration dy/dx tolerance 117.96678 10.64678 3 8.816784 7.32 1.83 4 8.359284 0.4575 8.244909 0.114375 6 8.216315 0.028594 8.209167 0.007148 8 8.20738 0.001787 9 8.206933 0.000447 when calculating f (x + ) and f (x + 110. .Test your program with a function you can take the derivative analytically (through calculus) 12 13 14 .Submit a validation of your program
