Using integration by parts, show that

() =()()

0

0

where () is integrable in [0, t], and Z(t) is a Brownian or Weiner process.

[10 marks]

[Hint: Use Ito's formula =

+

+1

2

2

2 ()2, select

(,) appropriately]

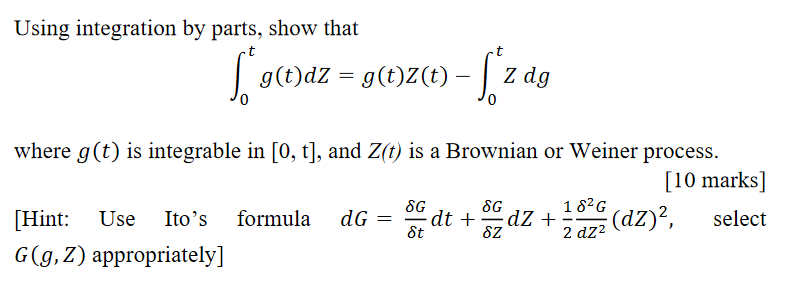
Using integration by parts, show that t g(t)dz = g(t)Z(t) - z dg 0 0 where g (t) is integrable in [0, t], and Z(t) is a Brownian or Weiner process. [10 marks] SG 6G [Hint: Use Ito's formula dG = dz + 16'G dt + (dz) 2, select St SZ 2 dz2 G(g, Z) appropriately]