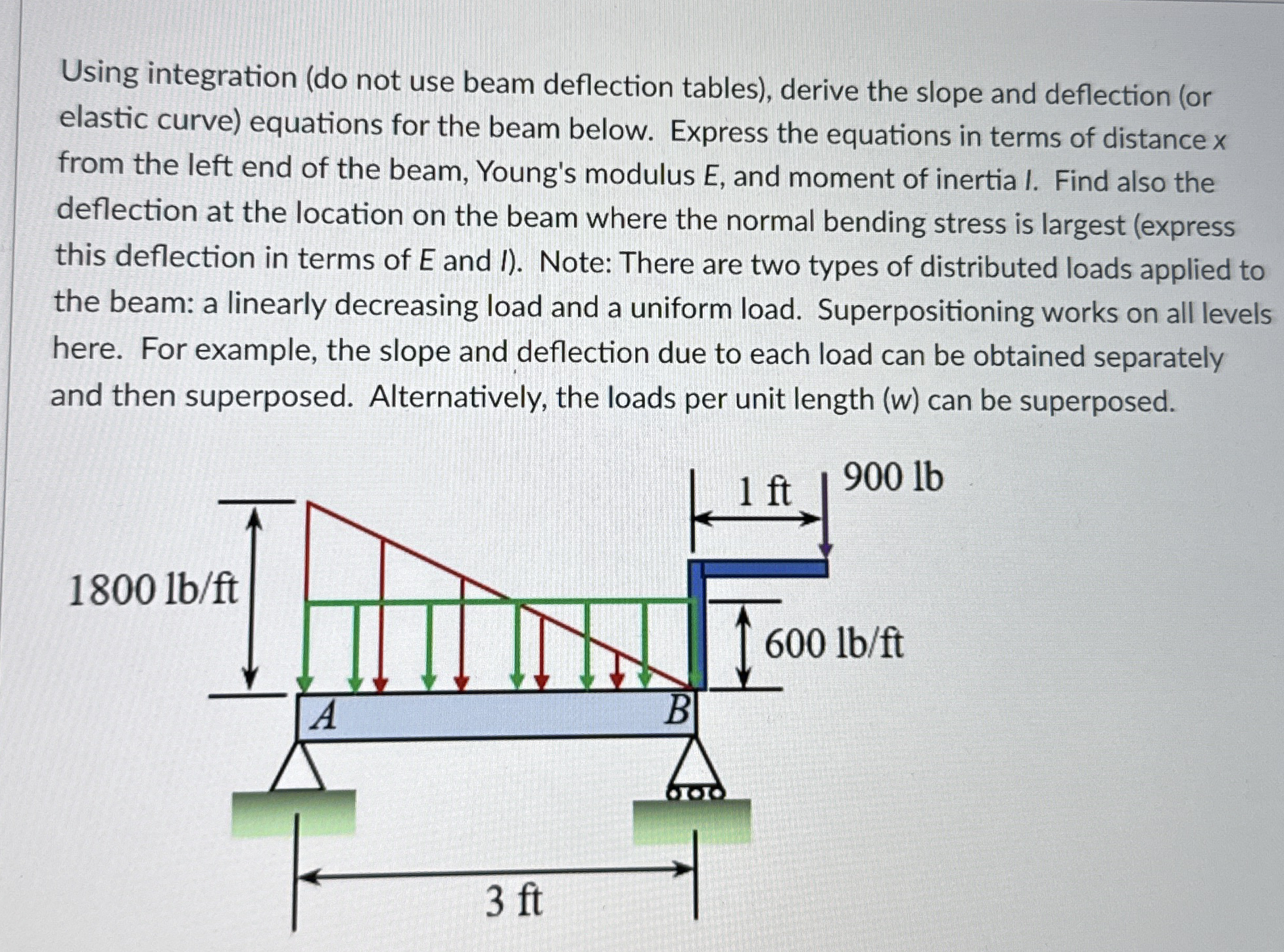
Question: Using integration ( do not use beam deflection tables ) , derive the slope and deflection ( or elastic curve ) equations for the beam
Using integration do not use beam deflection tables derive the slope and deflection or elastic curve equations for the beam below. Express the equations in terms of distance from the left end of the beam, Young's modulus E and moment of inertia I. Find also the deflection at the location on the beam where the normal bending stress is largest express this deflection in terms of and I Note: There are two types of distributed loads applied to the beam: a linearly decreasing load and a uniform load. Superpositioning works on all levels here. For example, the slope and deflection due to each load can be obtained separately and then superposed. Alternatively, the loads per unit length can be superposed.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


