1. Using lab 6 part 2, what would be the minimum required capacity at each workstation to maximize weekly profit? (Round answers to the nearest whole number)

   Workstation V -

   Workstation W -

   Workstation X -

   Workstation Y -

   Workstation Z -

10 points

QUESTION 5

1. Using lab 6 part 2, how much would you be willing to pay for an additional 100 minutes of capacity on workstation W?

   	A.	$129
   	B.	$86
   	C.	$0
   	D.	$100

10 points

QUESTION 6

1. Using lab 6 part 2, what is the amount of each product that would be produced if workstation capacities are set at 3,000 minutes? (Round your answer to the nearest whole number)

   Product A -

   Product B -

   Product C -

   Product D -

This is all the info needed

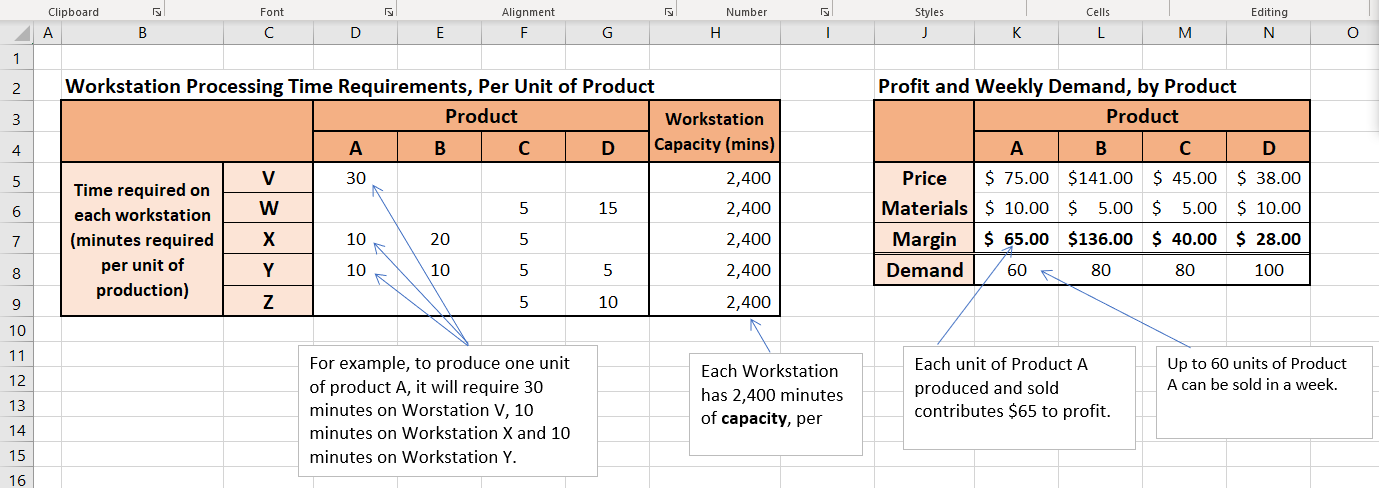
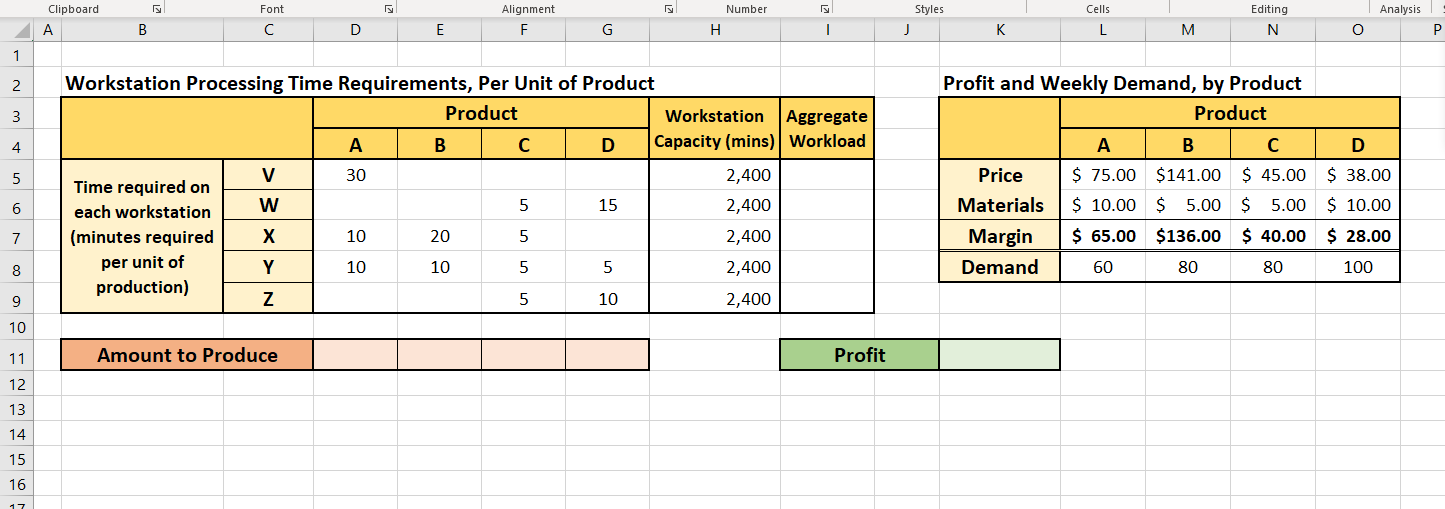
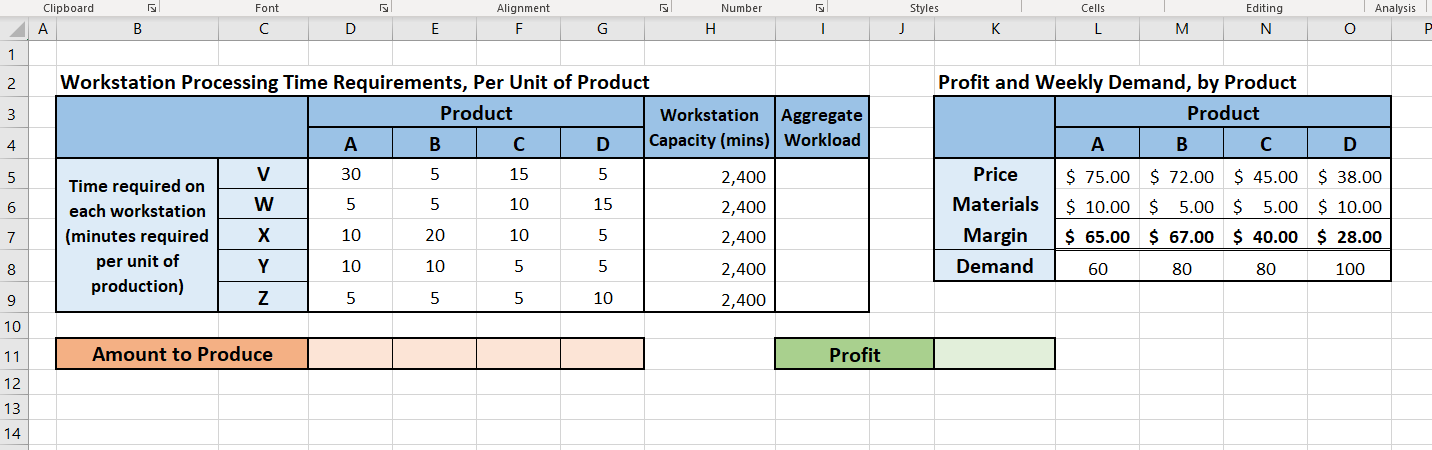
Problem 1: (Based on example 4.2 of the textbook, p.85) Consider a firm that produces and sells four products (A, B, C, and D), each of which will require production time on a combination of five workstations (V, W, X, Y, Z). Relevant data is provided in the 'Problem 1 - Data' worksheet. Take some time to understand the context; the Lab Tutor will help explain the data in the tables. (Note that demand and capacity are per week). Question 1: If each workstation has 2,400 minutes of capacity per week (40 hours per week times 60 minutes per hour), and assuming no overtime, can all of the weekly demand for all four products be met? (Think about it for a minute, and/or make a manual calculation. Once you understand the question posed, use the 'Problem 1 - Model' worksheet, and set the amount to produce in cells D11:G11 to be equal to the demand for the respective products. Then, develop formulas to compute the 'Aggregate Workload' in cells 15:19, which should reference the amount to produce and the time required on the workstations. Use conditional formatting to see where workstation demand exceeds capacity.) Question 2: Which workstation is the bottleneck? How do we know? [Let's hear from Jonah). Question 3: Since all of the weekly demand for all four products cannot be met, then how much of each product should be produced if the goal is to maximize profit? (Think about it for a minute, and/or make a manual calculation. Once you understand the question posed, set up a profit function in cell K11 that incorporates the amount produced of each product (cells D11:611) and the margin per unit sold (cells L7:07). Then, experiment with different values for the production amounts and see how high you can get profit; remember to make sure that your Aggregate Workload constraint isn't violated!) In class, we will learn a simple way to determine the optimal (max profit) product mix that can be used when there is only one bottleneck workstation. However, for more complex problems, we will need to use Solver to find the optimal product mix. Question 4: Solver: What is the objective (the Target" cell)? What is the decision we are trying to make (the "By Changing..." cells)? What are the constraints? Questions 5: Solve the problem. Does the optimal Solution make sense? Why was all of Cand D produced, when they have the lowest margins? Problem 2: (A Modification of Problem 1, to Create Multiple Bottlenecks). Once again, set up the model to find the aggregate workloads and total profit. Question 1: Is it possible to meet all of demand? Which workstation(s) is (are) system constraints? Now use Solver to find the optimal solution. (You will need to add a constraint that all production quantities must be integers). Look at the optimal solution, see which products demand was not met for. Question 2: What happens if you remove the default constraint that requires that production quantities be greater than or equal to zero? Why? Challenging Questions: Question 3: What happens if we add a constraint that we must produce at least 80% of demand for each product? Question 4: Using the result from Question 1, how much would you be willing to pay for 100 minutes of additional capacity at Workstation V? How much would you be willing to pay for 100 minutes of additional capacity at Workstation Z instead of V? Clipboard A Font Alignment F. Number H Styles J Cells L Editing N B D G M O 1 2 3 4 5 Workstation Processing Time Requirements, Per Unit of Product Product Workstation A B D Capacity (mins) V 30 2,400 Time required on W 5 15 each workstation 2,400 (minutes required 10 20 5 2,400 per unit of Y 10 10 5 5 2,400 production) Z 5 10 2,400 Profit and Weekly Demand, by Product Product A B C D Price $ 75.00 $141.00 $ 45.00 $ 38.00 Materials $ 10.00 $ 5.00 $ 5.00 $ 10.00 Margin $ 65.00 $136.00 $ 40.00 $ 28.00 Demand 60 80 80 100 6 7 8 9 10 11 12 Up to 60 units of Product A can be sold in a week. For example, to produce one unit of product A, it will require 30 minutes on Worstation V, 10 minutes on Workstation X and 10 minutes on Workstation Y. Each Workstation has 2,400 minutes of capacity, per Each unit of Product A produced and sold contributes $65 to profit. 13 14. 15 16 Styles Editing Analysis Clipboard A Font Alignment F Number H Cells L B D E G | J K M N O 1 2 3 D 5 Profit and Weekly Demand, by Product Product A B C Price $ 75.00 $141.00 $ 45.00 Materials $ 10.00 $ 5.00 $ 5.00 Margin $ 65.00 $136.00 $ 40,00 Demand 60 80 80 Workstation Processing Time Requirements, Per Unit of Product Product Workstation Aggregate A B D Capacity (mins) Workload V 30 2,400 Time required on W 5 each workstation 15 2,400 (minutes required 10 20 5 2,400 per unit of Y 10 10 5 5 2,400 production) Z 5 10 2,400 $ 38.00 6 $ 10.00 7 $ 28.00 8 100 9 10 11 Amount to Produce Profit 12 13 14 15 16 Clipboard Number Styles Analysis Font Alignment F Cells L Editing N A B D E G H | J K M O P 1 2 3 4 5 Workstation Processing Time Requirements, Per Unit of Product Product Workstation Aggregate A B D Capacity (mins) Workload V 30 5 15 5 2,400 Time required on W 5 5 10 15 each workstation 2,400 (minutes required X 10 20 10 5 2,400 per unit of Y 10 10 5 5 2,400 production) Z 5 5 5 10 2,400 Profit and Weekly Demand, by Product Product A B D Price $ 75.00 $ 72.00 $ 45.00 $ 38.00 Materials $ 10.00 $ 5.00 S 5.00 $ 10.00 Margin $ 65.00 $ 67.00 $ 40.00 $28.00 Demand 60 80 80 100 6 7 8 9 10 11 Amount to Produce Profit 12 13 14