Using Linear programing POM/QM system to calculate maximum profit for the coffee shop.

Explain the solution result.

Variable:

Where: X1 = Numbers of hot coffee

X2= Number of blended ice coffee

X3= Number of ice coffee

X1,X2,X3>=0

Constraints

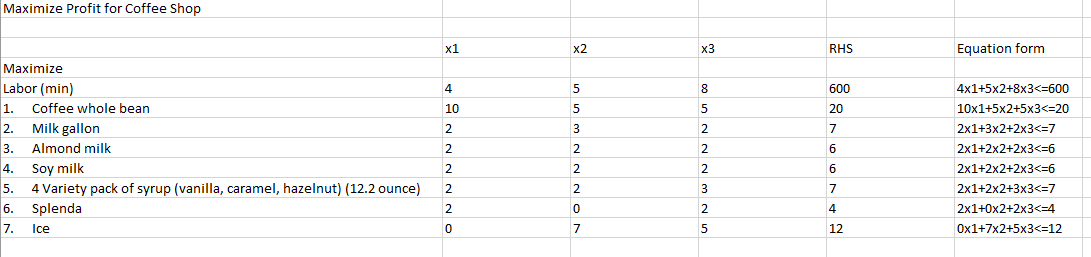
there were 8 constraints that affected the solution. They are:

1. 20 Coffee whole bean
2. 7 Milk gallon
3. 6 Almond milk
4. 6 Soy milk
5. 7 Variety pack of syrup (vanilla, caramel, hazelnut)
6. 4 box of Splenda
7. 12 bags of Ice
8. 600 minutes labor available

What is the Maximum?

The following step is to put in the maximum

X1= $2.36 per hot coffee.

X2= $2.56 per ice coffee

X3= $2.99 per blended ice coffee

Maximize Z = 2.36x1+2.56x2+2.99x3

subject to:

4x1+5x2+8x3

10x1+5x2+5x3

2x1+3x2+2x3

2x1+2x2+2x3

2x1+2x2+2x3

2x1+2x2+3x3

2x1+0x2+2x3

0x1+7x2+5x3

I need help putting these number into POM/QM

Maximize Profit for Coffee Shop x1 x2 x3 RHS Equation form 4 5 600 20 10 5 5 7 Maximize Labor (min) 1. Coffee whole bean 2. Milk gallon 3. Almond milk 4. Soy milk 5. Variety pack of syrup (vanilla, caramel, hazelnut) (12.2 ounce) 6. Splenda 7. Ice 2 3 2 2 CONNNN 6 4x1+5x2+8x3