Using Mathematica do the following: Edit the given code so that it will solve the Taveling Salesman Problem using the Brute Force method. Dont forget to return to the starting point. Be sure to print (one of) the cheapest path(s) and its corresponding cost. Then using the Timing command in Mathematica, compute the speed of the brute force algorithm for n = 1,2,3,4. Include these times as comments in your code. Recall that numNodes = n + 1. Brute Force Method: List every Hamiltonian cycle (a Hamiltonian cycle is a closed loop passing through each vertx exactly once), calculate the weight of each, then calculate the minimal (or lowest cost) cycle. The Traveling Salesman Problem: Given a complete network with n+1 verticies, what is the shortest path through the network which starts at some vertex, visists every vertex exactly once, then returns to the starting vertex? Use the following weights: 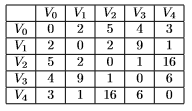The given code: SP = {{1}}; LP = {};

numNodes = 5;

LPpathLengths = 0;

While[LPpathLengths

SP = {{1}} LP = {{1,2},{1,3},{1,4},{1,5}} SP = {{1,2},{1,3},{1,4},{1,5}} LP = {{1,2,3},{1,2,4},{1,2,5},{1,3,2},{1,3,4},{1,3,5},{1,4,2},{1,4,3},{1,4,5},{1,5,2},{1,5,3},{1,5,4}} SP = {{1,2,3},{1,2,4},{1,2,5},{1,3,2},{1,3,4},{1,3,5},{1,4,2},{1,4,3},{1,4,5},{1,5,2},{1,5,3},{1,5,4}} LP = {{1,2,3,4},{1,2,3,5},{1,2,4,3},{1,2,4,5},{1,2,5,3},{1,2,5,4},{1,3,2,4},{1,3,2,5},{1,3,4,2},{1,3,4,5},{1,3,5,2},{1,3,5,4},{1,4,2,3},{1,4,2,5},{1,4,3,2},{1,4,3,5},{1,4,5,2},{1,4,5,3},{1,5,2,3},{1,5,2,4},{1,5,3,2},{1,5,3,4},{1,5,4,2},{1,5,4,3}} SP = {{1,2,3,4},{1,2,3,5},{1,2,4,3},{1,2,4,5},{1,2,5,3},{1,2,5,4},{1,3,2,4},{1,3,2,5},{1,3,4,2},{1,3,4,5},{1,3,5,2},{1,3,5,4},{1,4,2,3},{1,4,2,5},{1,4,3,2},{1,4,3,5},{1,4,5,2},{1,4,5,3},{1,5,2,3},{1,5,2,4},{1,5,3,2},{1,5,3,4},{1,5,4,2},{1,5,4,3}} LP = {{1,2,3,4,5},{1,2,3,5,4},{1,2,4,3,5},{1,2,4,5,3},{1,2,5,3,4},{1,2,5,4,3},{1,3,2,4,5},{1,3,2,5,4},{1,3,4,2,5},{1,3,4,5,2},{1,3,5,2,4},{1,3,5,4,2},{1,4,2,3,5},{1,4,2,5,3},{1,4,3,2,5},{1,4,3,5,2},{1,4,5,2,3},{1,4,5,3,2},{1,5,2,3,4},{1,5,2,4,3},{1,5,3,2,4},{1,5,3,4,2},{1,5,4,2,3},{1,5,4,3,2}} Final Output = {{1, 2, 3, 4, 5}, {1, 2, 3, 5, 4}, {1, 2, 4, 3, 5}, {1, 2, 4, 5, 3}, {1, 2, 5, 3, 4}, {1, 2, 5, 4, 3}, {1, 3, 2, 4, 5}, {1, 3, 2, 5, 4}, {1, 3, 4, 2, 5}, {1, 3, 4, 5, 2}, {1, 3, 5, 2, 4}, {1, 3, 5, 4, 2}, {1, 4, 2, 3, 5}, {1, 4, 2, 5, 3}, {1, 4, 3, 2, 5}, {1, 4, 3, 5, 2}, {1, 4, 5, 2, 3}, {1, 4, 5, 3, 2}, {1, 5, 2, 3, 4}, {1, 5, 2, 4, 3}, {1, 5, 3, 2, 4}, {1, 5, 3, 4, 2}, {1, 5, 4, 2, 3}, {1, 5, 4, 3, 2}}

Volo vi | 2 | 0 | 2 | 9 | 1 2520 1 16 V3910 6 V31 16 60 0 25 3