Using Matlab and show output

create a script in Matlab that will estimate the solution for an ordinary differential equation using the RK4 method outlined above. Below is some code to help you get started:

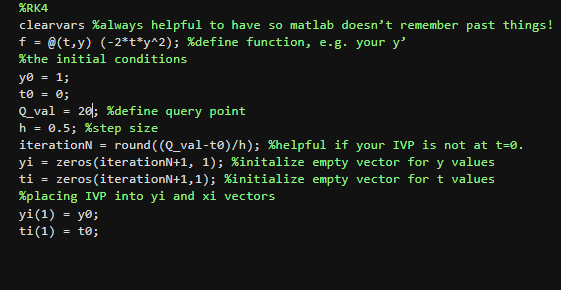
\%RK4 clearvars \%always helpful to have so matlab doesn't remember past things! f=@(t,y)(2ty2); \%define function, e.g. your y \%the initial conditions Using the RK4 method, give the numerical approximation for the IVP: y=ty; y(0)=e; with a step size of h=0.5 for the point at t=20. How does this compare to Euler's Method (e.g. simply using the k1 values to approximate this ODE)?. The exact solution to the IVP above is y(t)=et2/2+1. In a single figure, plot the results of RK4, Euler methods and the exact function (thus, your plot should contain 3 lines). To show the full Y-range, the Y-axis should be plotted using a log-scale, however the X-axis should remain linear. To do this, type "set(gca, 'YScale','log')" on the line below that used to create the plot. Make sure that your figure has a legend that describes what each line corresponds to. Suppose we have the initial value problem (IVP): y=f(t,y);y(t)=yo where y is the time derivative of the function y, i.e. y=dtdy.y is an unknown function of time t, which we would like to approximate; we are told that y, the rate at which y changes, is a function of t and of y itself. At the initial time to the corresponding y value is y0. The function f and the data to,y0 are given. We want to 'step' through the function to find a numerical approximation at some time, t. Choose a step size, h, such that h>0 and define: yn+1=yn+6h(k1+2k2+2k3+k4)tn+1=tn+h for n=0,1,2,3,, using: k1=f(tn,yn)k2=f(tn+2h,yn+2hk1)k3=f(tn+2h,yn+2hk2) 1 k4=f(tn+h,yn+hk3) Here yn+1 is the RK4 approximation of y(tn+1), and the next value (yn+1) is determined by the present value (yn) plus the weighted average of four increments, where each increment is the product of the size of the interval, h, and an estimated slope specified by function f on the right-hand side of the differential equation. - k1 is the increment based on the slope at the beginning of the interval, using y. - k2 is the increment based on the slope at the midpoint of the interval, using y+2hk1; - k3 is again the increment based on the slope at the midpoint, but now using y+2hk2; - k4 is the increment based on the slope at the end of the interval, using y+hk3