Using matlab

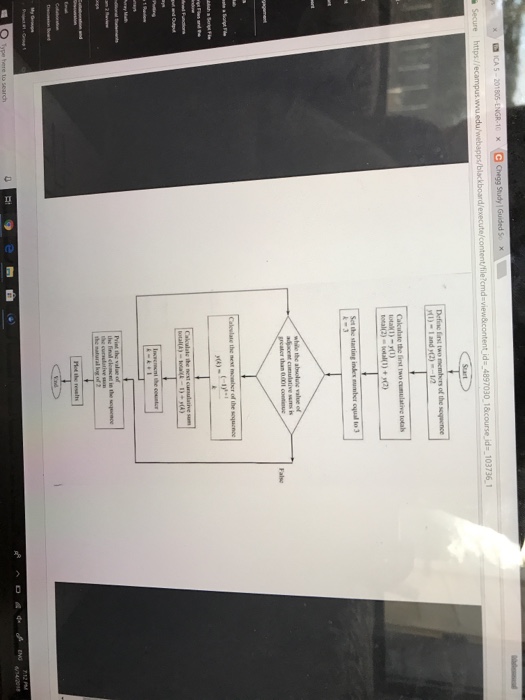
For this week's ICA, we will be looking at a particular mathematical series. This series c to the natural log of 2 and is given below: ?(-1)-1-1+11+1-...=ln(2):06931471806 -= 1--+ +--...-In(2) = 0.693 1471806 As you can see, this summation goes to infinity. You probably don't want to continue this series tha. far Instead of continuing on to infinity and beyond, you can set a limit as to how accurate you would like your answer to be. So, for this problem, we do not know how many iterations it will take to get to a certain accuracy, but we do know a condition we want to continue to before stopping. In this situation, we want to use a while loop (see zyBook chapter 12 and the Loops PowerPoint). For this ICA, do the following: Use a while loop to calculate the values in this series until the absolute value of consecutive sums is less than or equal to 0.001. Ensure that you are creating a vector to store each term in the series Use an fprintf to display the value of the series after the condition in part a. is met. Compare this to the actual value of In(2). Also display the number of terms needed for convergence to that level of accuracy. Use 4 decimal places for the value of the series and the In(2) value in your frpintf statement(s) a. b. c. Create a plot of the number of terms (horizontal axis) versus the series values (vertical axis). Your horizontal axis should be on a log scale. The series values are the vector that you created in part a. This plot will show you how the series converges as the number of terms increases A flowchart is provided for you on the following page to guide you through completing this problem. Flowcharts are useful tools to help develop a strategy for solving a problem before typing any code