Using MatLab to solve this problem using techniques that involve user defined functions and preprogrammed functions and no loops of any sort to solve this problem:

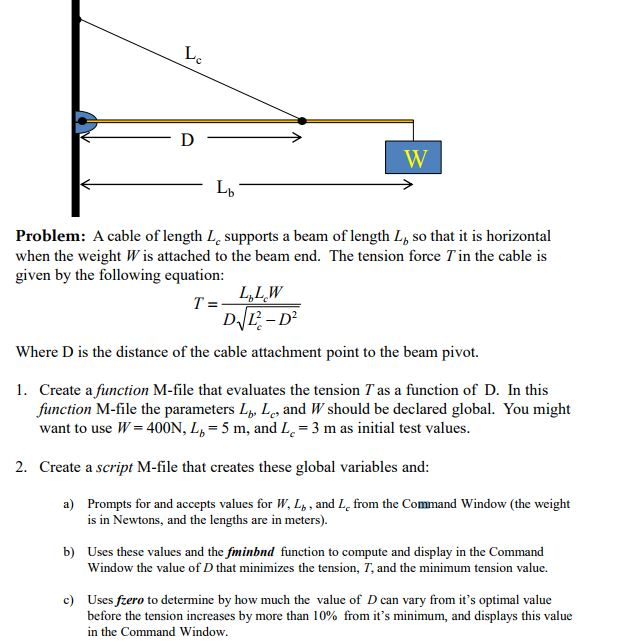
Le Problem: A cable of length Lc supports a beam of length L, so that it is horizontal when the weight Wis attached to the beam end. The tension force Tin the cable is given by the following equation Where D is the distance of the cable attachment point to the beam pivot. 1. Create a function M-file that evaluates the tension T as a function of D. In this function M-file the parameters L, L, and W should be declared global. You might want to use W 400N, L,5 m, and Lc 3 m as initial test values 2. Create a script M-file that creates these global variables and a) Prompts for and accepts values for W, Lb, and Lc from the Command Window (the weight is in Newtons, and the lengths are in meters). b) Uses these values and the fiminbnd function to compute and display in the Command Window the value of D that minimizes the tension, T, and the minimum tension valuc. c) Uses ftero to determine by how much the value of D can vary from it's optimal value before the tension increases by more than 10% from it's minimum, and displays this value in the Command Window Le Problem: A cable of length Lc supports a beam of length L, so that it is horizontal when the weight Wis attached to the beam end. The tension force Tin the cable is given by the following equation Where D is the distance of the cable attachment point to the beam pivot. 1. Create a function M-file that evaluates the tension T as a function of D. In this function M-file the parameters L, L, and W should be declared global. You might want to use W 400N, L,5 m, and Lc 3 m as initial test values 2. Create a script M-file that creates these global variables and a) Prompts for and accepts values for W, Lb, and Lc from the Command Window (the weight is in Newtons, and the lengths are in meters). b) Uses these values and the fiminbnd function to compute and display in the Command Window the value of D that minimizes the tension, T, and the minimum tension valuc. c) Uses ftero to determine by how much the value of D can vary from it's optimal value before the tension increases by more than 10% from it's minimum, and displays this value in the Command Window