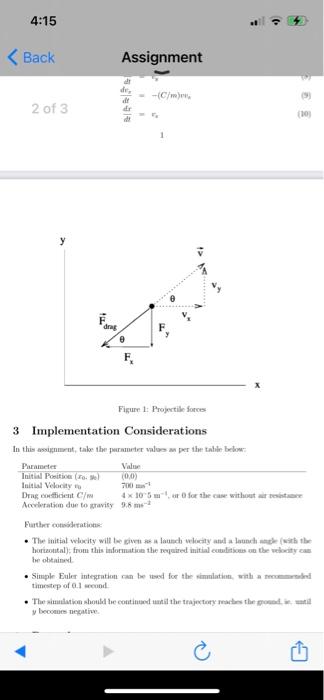
Question: Using python 1 Introduction The aim of this project is to determine the trajectory of a cannot shell including the effects of air resistance, lising
Using python

1 Introduction The aim of this project is to determine the trajectory of a cannot shell including the effects of air resistance, lising trimerical methods. You will be required to plotut the trajectories to determine the launch angle required to hit a target at a specified distance, and to determine the launch angle that gives maximum ratige 2 Theory The equations governing the motion of a projectile of mine mare dra dro where and are the coordinates of the projectile at time, and F. and Fare the components of the force in the any direction Thon drag force is proportional to the square of the speed of the projectile dy 13) F = CP ( From Figure 1 below, it should be evident that: 15 = Fare ces # = ( Fare vin 0 - (One) Cm 16 17 Therefore, the equations to be solved are: dey - 9-(C/me dy dll de -(C/mee, d (8) 19 (10) dr 1 drag F F, Figure 1: Projectile forces 3 Implementation Considerations In this assignment, take the parameter values as per the table below Parameter Value Initial Position to yo) (0,0) Initial Velocity 700 Drag coefficient C/m 4 x 10-5 m, or for the case without air resistance Acceleration due to gravity 9.8 ms? Further considerations: The initial velocity will be given as a larunch velocity and a launch angle with the horizontal), from this information the required initial conditions on the velocity can be obtained Simple Euler integration can be used for the simulation, with a recommended timestop of 0.1 second The similation should be continued until the trajectory reaches the ground, c. until y becomes negative . 4. Determine the launch angle required to hit a target distant 20km from the launch point, both with and without air resistance. To do this, re-write your program as a function that takes the launch angle as an argument and returns the range (plotting is no longer required). Use this function in a bisection algorithm to home in on the angle that results in a range of 20km, continuing to an angular accuracy of 0.1. Note that in general a given range can be obtained for two launch angles so choose your initial bisection interval with care. Also, plot the resulting trajectories on the same graph. 4:14 drag Figure 1: Projectile forces 3 Implementation Considerations In this it take the value per the table below Parameter Vale Initi Poti Initial Velocity Drug confident C/ 4 x 10-50 for the without Acceleration due to hvity 9.8m Further coderations horizontal from this information the required initial to the city he obtained Simple Euler integration can be ted for the simmlution with a timestep of 0.1 cod The aluatko should be continued until the trajectory reaches the poolt y becomes negative 4. Determine the launch angle required to hit a target distant 20km from the launch point, both with and without air resistance. To do this, re-write your program as a function that takes the launch angle as an argument and returns the range (plotting is no longer required). Use this function in a bisection algorithm to home in on the angle that results in a range of 20km, continuing to an angular accuracy of 0.1. Note that in general a given range can be obtained for two launch angles so choose your initial bisection interval with care. Also, plot the resulting trajectories on the same graph. 1 Introduction The aim of this project is to determine the trajectory of a cannot shell including the effects of air resistance, lising trimerical methods. You will be required to plotut the trajectories to determine the launch angle required to hit a target at a specified distance, and to determine the launch angle that gives maximum ratige 2 Theory The equations governing the motion of a projectile of mine mare dra dro where and are the coordinates of the projectile at time, and F. and Fare the components of the force in the any direction Thon drag force is proportional to the square of the speed of the projectile dy 13) F = CP ( From Figure 1 below, it should be evident that: 15 = Fare ces # = ( Fare vin 0 - (One) Cm 16 17 Therefore, the equations to be solved are: dey - 9-(C/me dy dll de -(C/mee, d (8) 19 (10) dr 1 drag F F, Figure 1: Projectile forces 3 Implementation Considerations In this assignment, take the parameter values as per the table below Parameter Value Initial Position to yo) (0,0) Initial Velocity 700 Drag coefficient C/m 4 x 10-5 m, or for the case without air resistance Acceleration due to gravity 9.8 ms? Further considerations: The initial velocity will be given as a larunch velocity and a launch angle with the horizontal), from this information the required initial conditions on the velocity can be obtained Simple Euler integration can be used for the simulation, with a recommended timestop of 0.1 second The similation should be continued until the trajectory reaches the ground, c. until y becomes negative . 4. Determine the launch angle required to hit a target distant 20km from the launch point, both with and without air resistance. To do this, re-write your program as a function that takes the launch angle as an argument and returns the range (plotting is no longer required). Use this function in a bisection algorithm to home in on the angle that results in a range of 20km, continuing to an angular accuracy of 0.1. Note that in general a given range can be obtained for two launch angles so choose your initial bisection interval with care. Also, plot the resulting trajectories on the same graph. 4:14 drag Figure 1: Projectile forces 3 Implementation Considerations In this it take the value per the table below Parameter Vale Initi Poti Initial Velocity Drug confident C/ 4 x 10-50 for the without Acceleration due to hvity 9.8m Further coderations horizontal from this information the required initial to the city he obtained Simple Euler integration can be ted for the simmlution with a timestep of 0.1 cod The aluatko should be continued until the trajectory reaches the poolt y becomes negative 4. Determine the launch angle required to hit a target distant 20km from the launch point, both with and without air resistance. To do this, re-write your program as a function that takes the launch angle as an argument and returns the range (plotting is no longer required). Use this function in a bisection algorithm to home in on the angle that results in a range of 20km, continuing to an angular accuracy of 0.1. Note that in general a given range can be obtained for two launch angles so choose your initial bisection interval with care. Also, plot the resulting trajectories on the same graph