using Python

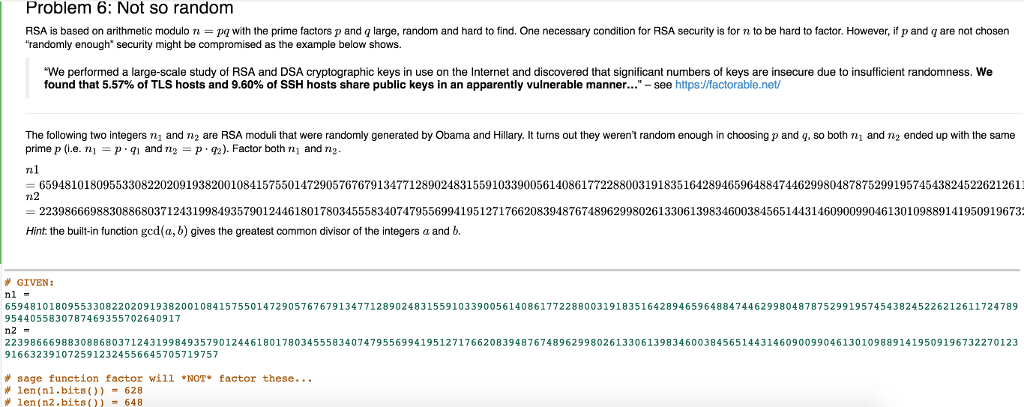
Problem 6: Not so random RSA is based on arithmetic modulo n pq with the prime factors p and q large, random and hard to find. One necessary conditionfor RSA security is for n to be hard to factor. However, if p and are not chosen randomly enough" security might be compromised as the example below shows. "We performed a large-scale study of RSA and DSA cryptographic keys in use on the Internet and discovered that significant numbers of keys are insecure due to insufficient randomness. We found that 5.57% of TLS hosts and 9.60% of SSH hosts share public keys in an apparently vulnerable manner "-see https://factorable-net/ q, so both ni and ended up with the same The following two integers n1 and n2 are RSA moduli that were randomly generated by Obama and Hillary. It turns out they weren't random enough in choosing p and prime p (i.e. ni-p and n p2). Factor both n and n2 nl 65948101809553308220209193820010841575501472905767679134771289024831559103390056140861772288003191835164289465964884744629980487875299195745438245226212611 n2 22398666988308868037124319984935790124461801780345558340747955699419512717662083948767489629980261330613983460038456514431460900990461301098891419509196735 Hint. the built-in function gcd(a, b) gives the greatest common divisor of the integers a and b GIVEN 65948101809553308220209193820010841575501472905767679134771289024831559103390056140861772288003191835164289465964884 44629980487875299195745438245226212611724789 9544055830787469355702640917 n2 22398666988308868037124319984935790124461801780345558340747955699419512717662083948767489629980261330613983460038456514431460900990461301098891419509196732270123 9166323910725912324556645705719757 sage function factor will 'NOT factor these... W len(n1.bits 628 rP len(n2.bits()) ?648 Problem 6: Not so random RSA is based on arithmetic modulo n pq with the prime factors p and q large, random and hard to find. One necessary conditionfor RSA security is for n to be hard to factor. However, if p and are not chosen randomly enough" security might be compromised as the example below shows. "We performed a large-scale study of RSA and DSA cryptographic keys in use on the Internet and discovered that significant numbers of keys are insecure due to insufficient randomness. We found that 5.57% of TLS hosts and 9.60% of SSH hosts share public keys in an apparently vulnerable manner "-see https://factorable-net/ q, so both ni and ended up with the same The following two integers n1 and n2 are RSA moduli that were randomly generated by Obama and Hillary. It turns out they weren't random enough in choosing p and prime p (i.e. ni-p and n p2). Factor both n and n2 nl 65948101809553308220209193820010841575501472905767679134771289024831559103390056140861772288003191835164289465964884744629980487875299195745438245226212611 n2 22398666988308868037124319984935790124461801780345558340747955699419512717662083948767489629980261330613983460038456514431460900990461301098891419509196735 Hint. the built-in function gcd(a, b) gives the greatest common divisor of the integers a and b GIVEN 65948101809553308220209193820010841575501472905767679134771289024831559103390056140861772288003191835164289465964884 44629980487875299195745438245226212611724789 9544055830787469355702640917 n2 22398666988308868037124319984935790124461801780345558340747955699419512717662083948767489629980261330613983460038456514431460900990461301098891419509196732270123 9166323910725912324556645705719757 sage function factor will 'NOT factor these... W len(n1.bits 628 rP len(n2.bits()) ?648