using python

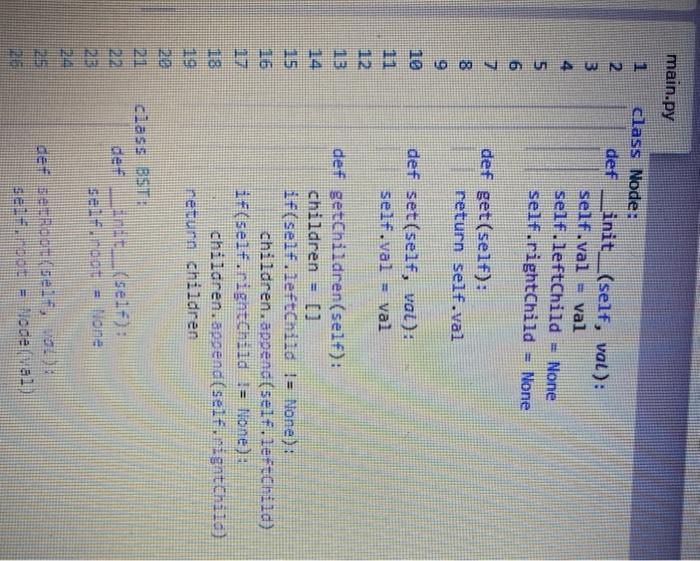
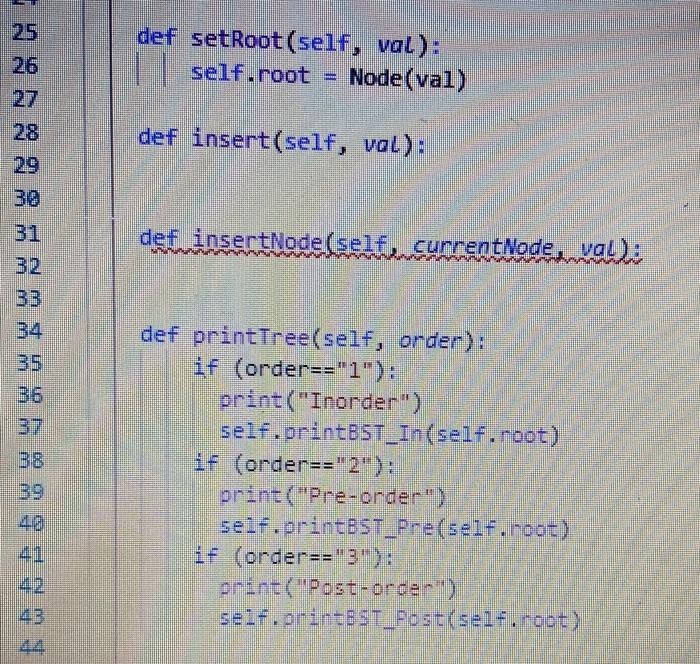
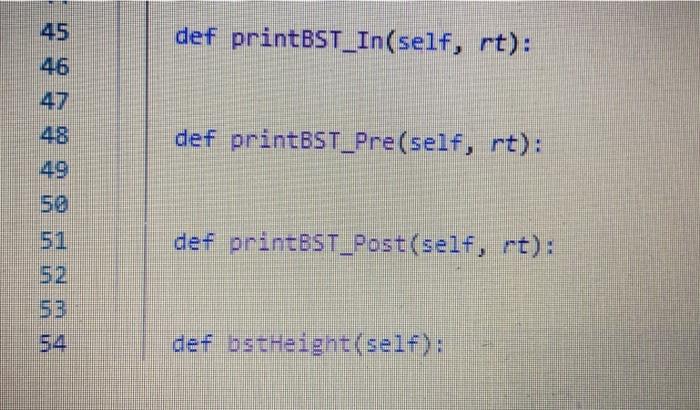
Problem: A binary search tree(BST) relies on the property that keys that are less than the parent are found in the left subtree, and keys that are greater than(or equal) the parent are found in the right subtree. Implement a BST with the following basic components 1. Create a BST for a list of data (= 10,5. 8. 2. 4. 12. 11.4.9. 15) use insert(value) function 2. Print the values in inorder, preorder, and post order 3. Compute the heigh of the BST Extra credit: Write delNode(val) function to delete any node from the BST. Note: Feel free to use the given helper code or write your own main.py 1 class Node: 2 definit _(self, val): 3 self.val - val 4 self.leftChild = None 5 self.rightChild = None 6 def get(self): 8 return self.val 10 11 def set(self, val): self.val = val 1 13 16 def getChildren(self): children if(self. leftChild 1= None): children. append(self.leftchild) if(self.nightChild = None): chilaren.append(self.nzgnt Child) netunn children No ca EN N class BST: definit__(self): sei.root = None def serRootself, se:.00 = Node (val) def setRoot(self, val): self.root Node(val) 28 def insert(self, val): 31 def insertNode(self, currentNode. val): 32 S01 3 B def printTree(self, order): if (order=="1"): print("Inorder") self.printBST_In(self.root) if (order=="2"): print("Pre-order") self.printBST_Pre(self.root) if (order=="3"): print("Post-order) self.printBST_Post(self.root) def printBST_In(self, rt): 45 46 47 48 49 def printBST_Pre(self, rt): def printBST_Post(self, rt): def bstHeight(self)