Using R to solve question 1.

These are all the information we need :)

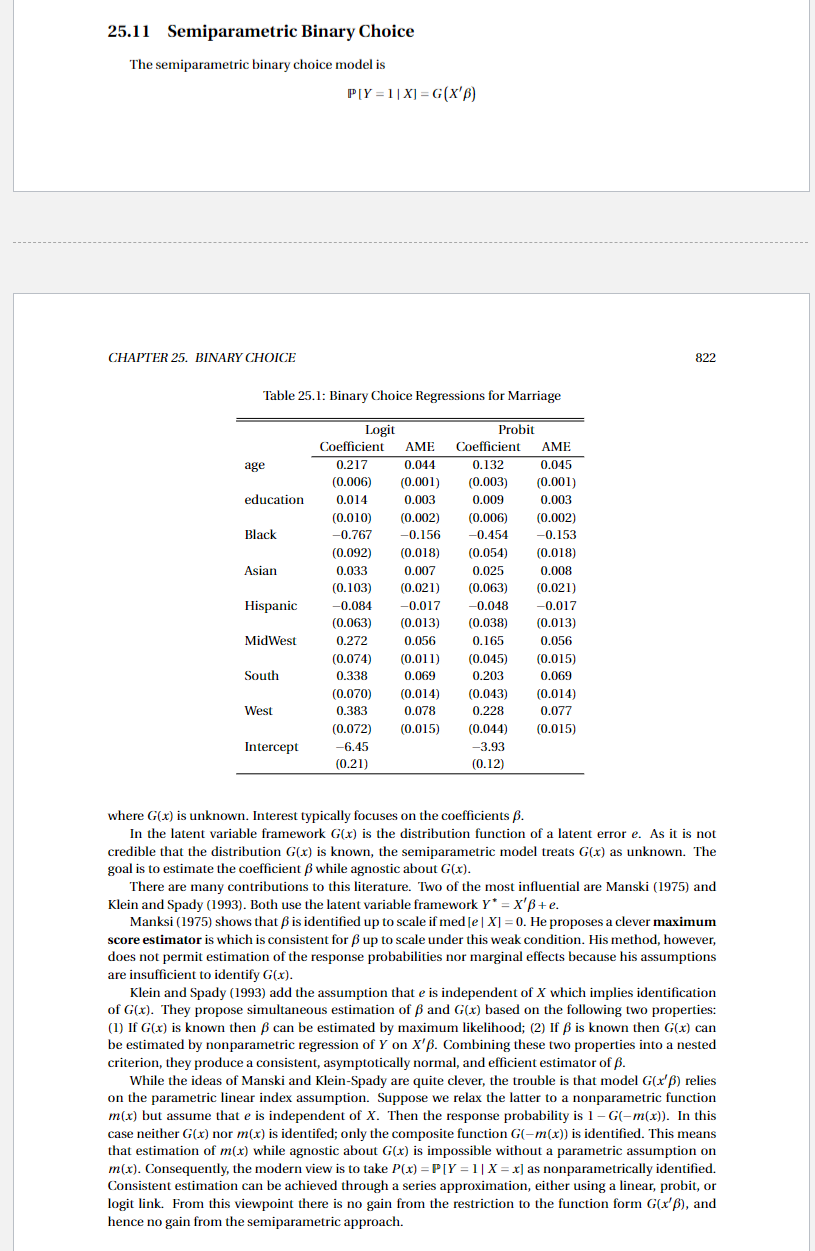
PLEASE READ THE FOOTNOTES AT THE BOTTOM OF THIS PAGE BEFORE CONTINUING 1. Reproduce Table 25.1 from BHE', p. 822. 2. ISLR', p. 191, Problem 6. 3. ISLR, p. 220, Problem 5. The Default data set can be found in the ISLR2 package. 1Hansen, B. Econometrics. You must use the "Final Public Draft" edition of this text, which is available in the Readings directory on Canvas. "You must use the Second Edition of this text (from 2021), which is available in the Readings directory on Canvas.25.11 Semiparametric Binary Choice The semiparametric binary choice model is P[Y = 1[ X] = G(X'S) CHAPTER 25. BINARY CHOICE 822 Table 25.1: Binary Choice Regressions for Marriage Logit Probit Coefficient AME Coefficient AME age 0.217 0.04 0.132 0.045 (0.006) (0.001) (0.003) (0.001) education 0.014 0.003 0.009 0.003 (0.010) 0.002) (0.006) 0.002) Black -0.767 -0.156 -0.454 -0.153 (0.092) (0.018) (0.054) (0.018) Asian 0.033 0.007 0.025 0.008 (0.103) (0.021) (0.063) (0.021) Hispanic -0.084 -0.017 -0.048 -0.017 (0.063) (0.013) (0.038) (0.013) MidWest 0.272 0.056 0.165 0.056 (0.074) (0.011) (0.045) (0.015) South 0.338 0.069 0.203 0.069 (0.070) (0.014) (0.043) (0.014) West 0.383 0.078 0.228 0.077 (0.072) (0.015) (0.044) (0.015) Intercept -6.45 -3.93 (0.21) (0.12) where G(x) is unknown. Interest typically focuses on the coefficients B. In the latent variable framework G(x) is the distribution function of a latent error e. As it is not credible that the distribution G(x) is known, the semiparametric model treats G(x) as unknown. The goal is to estimate the coefficient f while agnostic about G(x). There are many contributions to this literature. Two of the most influential are Manski (1975) and Klein and Spady (1993). Both use the latent variable framework Y* = X'S + e. Manksi (1975) shows that f is identified up to scale if med [e | X] = 0. He proposes a clever maximum score estimator is which is consistent for p up to scale under this weak condition. His method, however, does not permit estimation of the response probabilities nor marginal effects because his assumptions are insufficient to identify G(x). Klein and Spady (1993) add the assumption that e is independent of X which implies identification of G(x). They propose simultaneous estimation of p and G(x) based on the following two properties: (1) If G(x) is known then p can be estimated by maximum likelihood; (2) If f is known then G(x) can be estimated by nonparametric regression of Y on Xp. Combining these two properties into a nested criterion, they produce a consistent, asymptotically normal, and efficient estimator of B. While the ideas of Manski and Klein-Spady are quite clever, the trouble is that model G(x'S) relies on the parametric linear index assumption. Suppose we relax the latter to a nonparametric function m(x) but assume that e is independent of X. Then the response probability is 1 - G(-m(x)). In this case neither G(x) nor m(x) is identifed; only the composite function G(-m(x)) is identified. This means that estimation of m(x) while agnostic about G(x) is impossible without a parametric assumption on m(x). Consequently, the modern view is to take P(x) = P[Y = 1 | X = x] as nonparametrically identified. Consistent estimation can be achieved through a series approximation, either using a linear, probit, or logit link. From this viewpoint there is no gain from the restriction to the function form G(x'S), and hence no gain from the semiparametric approach