Question: Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph

the graph using first two and then four rectangles. f(x) = x3

$between x = O and x = 2 \\3 n n S$

ak =6 and _ by = 42, find the following values. k

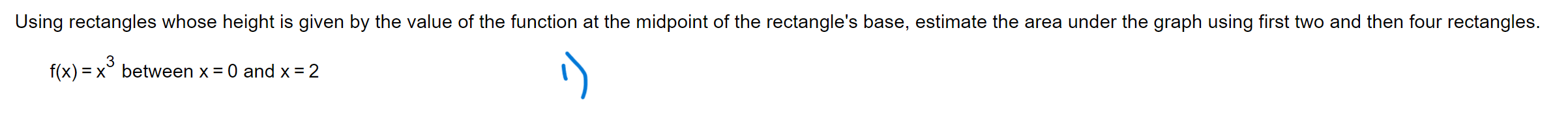
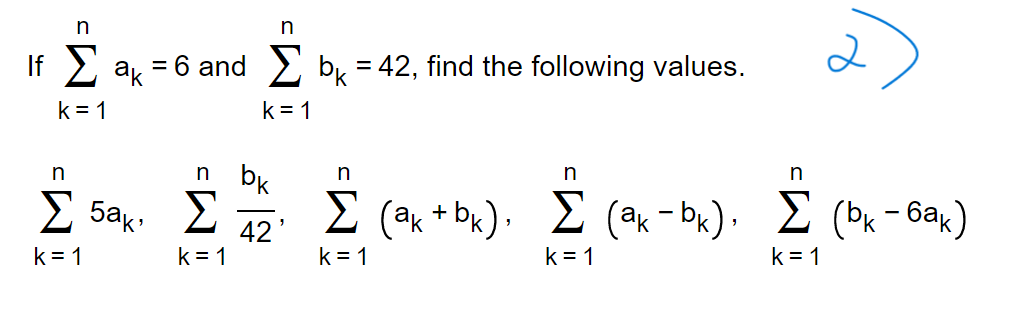
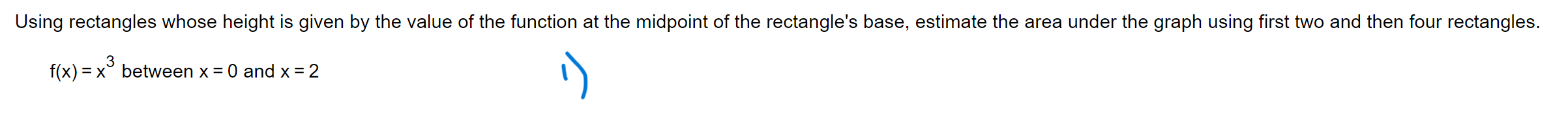
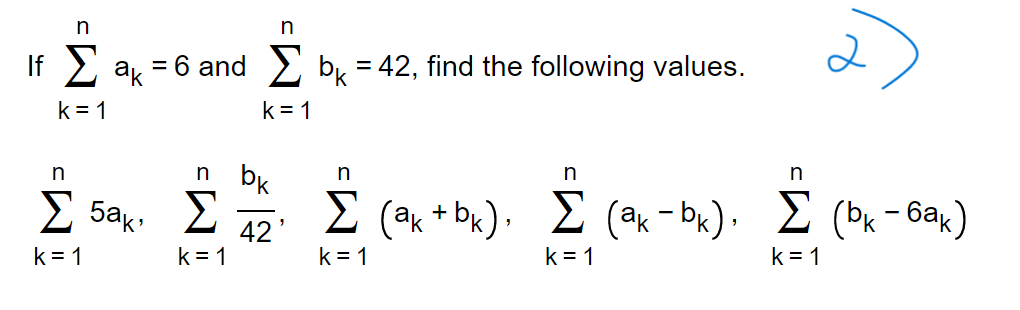
1 K = 14 The functions f and g are integrable and

Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph using first two and then four rectangles. f(x) = x3 between x = O and x = 2 \\3 n n S ak =6 and _ by = 42, find the following values. k = 1 k = 1 n n bk n n n 5ak. E 42 2 (ak + bk), _ (ak- bk), Z (bK - Gak) k = 1 K = 1 K = 1 k = 1 K = 14 The functions f and g are integrable and f(x)dx = 4, f(x)dx = - 4, and g(x)dx =6. Use these to complete parts (a) through (f). 2 . . . 4 a. J f( x ) dx = 0 3 4 ( Simplify your answer.) 2 b. g(x)dx = 7 (Simplify your answer.)8 9 Suppose that f is integrable, and that If(z)dz = 3 and If(z)dz = 6. Find the value of the following definite integrals. m 9 (a) If(z)dz = E (Type an integer or a decimal.) 8 \fUse a definite integral to find the area of the region between the given curve and the x-axis on the interval [0, b]. y = 11x2 [0) The area is D. b What values of a and b maximize the value of [(12x - x2) dx? a (Hint: Where is the integrand positive?) 7 a = D and b = D maximize the given integral. (Simplify your answer. Type a whole number.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Good afternoon, can you help me with those questions 1. A. Using two rectangles to estimate, the area under f(x) is approximately B. Using four rectangles to estimate, the area under f(x) is...

Estimate the area under the graph of x}: 4x3 between at: O and x: 6 using each finite approximation below. a. A lower sum with two rectangles of equal width b. A lower sum with tour rectangles of...

helppppppppp and then four rectangles Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph using first two...

I need help with this question please. Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph using first two...

Hello, Seeking guidance for this question that I encountered on a lab. Any assistance for this question or a point in the right direction is extremely appreciated! Thanks Using rectangles whose...

1- please help me with this problem. THANK YOU :) i will review. Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under...

Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph using first two and then four rectangles. f(x) =x-...

Using rectangles whose height is given by the value of the function at the midpoint of the rectangle's base, estimate the area under the graph using first two and then four rectangles. f(x) =x...

Fiona's Store had the following transactions during December, the last month of the accounting period (20 points): Sold merchandise on credit for $6,000, cost $4.000 terms I 10. n 30. 3 Purchased...

At the beginning of last year, you invested $4,000 in 80 shares of the Chang Corporation. During the year, Chang paid dividends of $5 per share. At the end of the year, you sold the 80 shares for $59...

Based on the Variable Cells Constraintsoptimal results and the sensitivity report, answer the following independent questions: ( b ) What is the least expensive redistribution plan for the vehicles?...

A hula hoop and solid disc of equal radii are rolled, from rest and without slipping, down an incline plane. Which one will reach the bottom of the inclined plane first? Explain.

(a) AB Hi-Fi has adopted a HR strategy; its overall plan is to hire the best and most flexible employees. How well does their current HR and payroll cycle align with this business strategy? (b)'Are...

During process 3.0 Calculate payroll at AB Hi-Fi, before the salary is deposited into the employees bank accounts by electronic funds transfer, the approval of the departmental manager is sought....

Read the narrative below and answer the following questions. Required (a) Based on the narrative above, what are the weaknesses in the system of internal control? (b) What enquiries should be made...