Using simple C++ programming (loop, while, do while, switch statement) to develop the algorithm for root finding using Newtons Method.

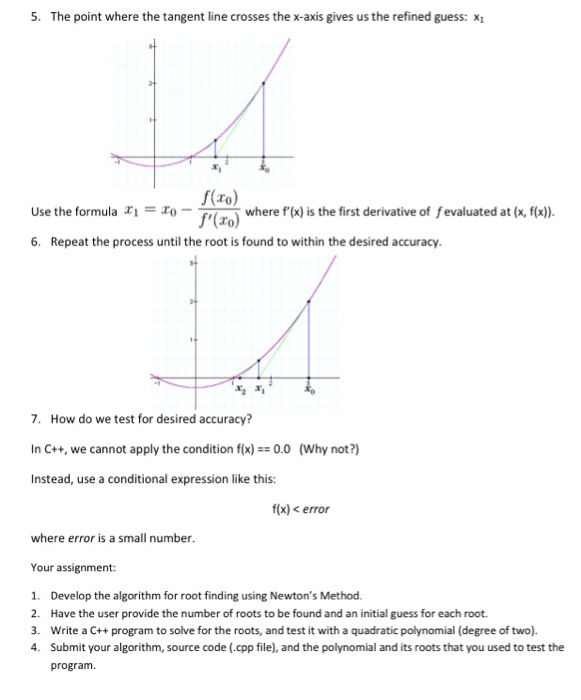
Newton's Method of Finding Roots of Polynomials A polynomial is expressed in the form: where the a's are coefficients for the powers-of-x terms. The last coefficient, a, is a constant term. Example: Objective: Find the roots of f(x). Roots are x values for which (x) 0. Things to note about polynomial functions: f(x) 2x2 -2x-4 ."Degree" of the polynomial is N (our example: 2nd degree polynomial) Degree is important because it tells us how many roots. A polynomial of degree N has N roots (which may be real or complex). Roots may also be repeated. (The two roots may be the same root!) If the polynomial is factored into linear terms, we can find the roots by inspection: f(x) 2x2- 2x-4-(2x-4)1) has roots 2x-4=0 x=2 and Let's automate the process by developing an algorithm that can be coded into a computer program Here are the steps of Newton's Method: 1. Guess a solution. Xo 2. Evaluate the function at xo: f(xo) 3. Is this the root? Yes if f(xo) 0; no otherwise. 4. If this is not the root, refine the guess by finding a line tangent to the function at the point (xO, f(x0)) and following that tangent line back to the x-axis: rx