Question: Using the change o f variables x = u 2 - v 2 , y = 7 u v t o evaluate the integral R
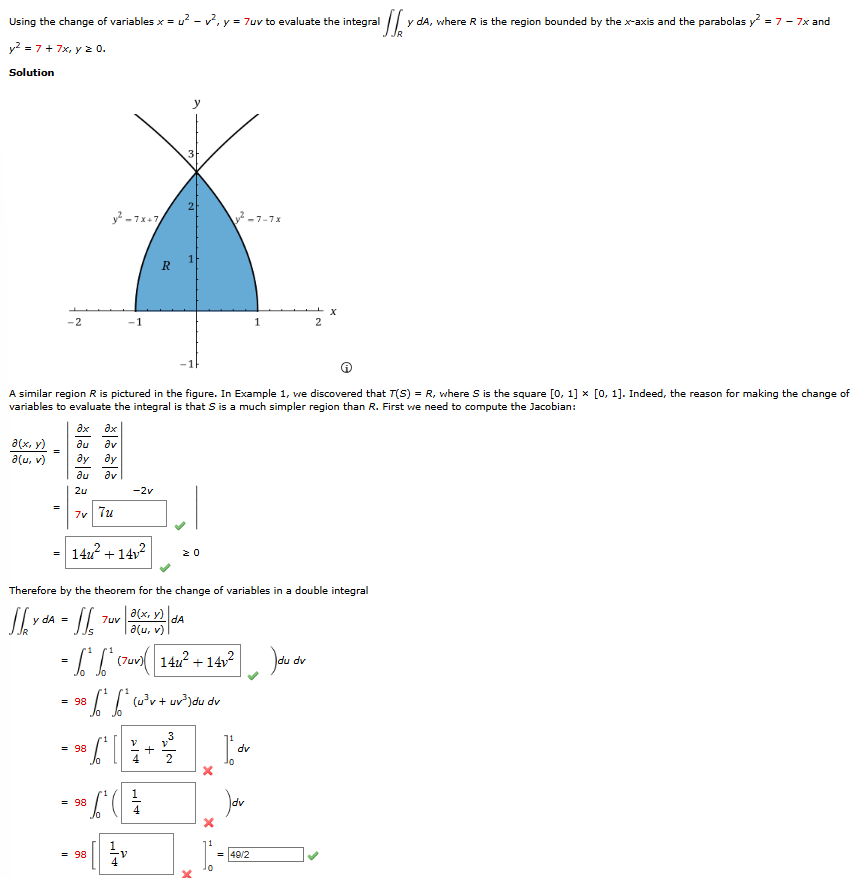
Using the change variables evaluate the integral ydA, where the region bounded the axis and the parabolas and
Solution
A similar region pictured the figure. Example discovered that where the square Indeed, the reason for making the change
variables evaluate the integral that a much simpler region than First need compute the Jacobian:
Therefore the theorem for the change variables a double integral
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


