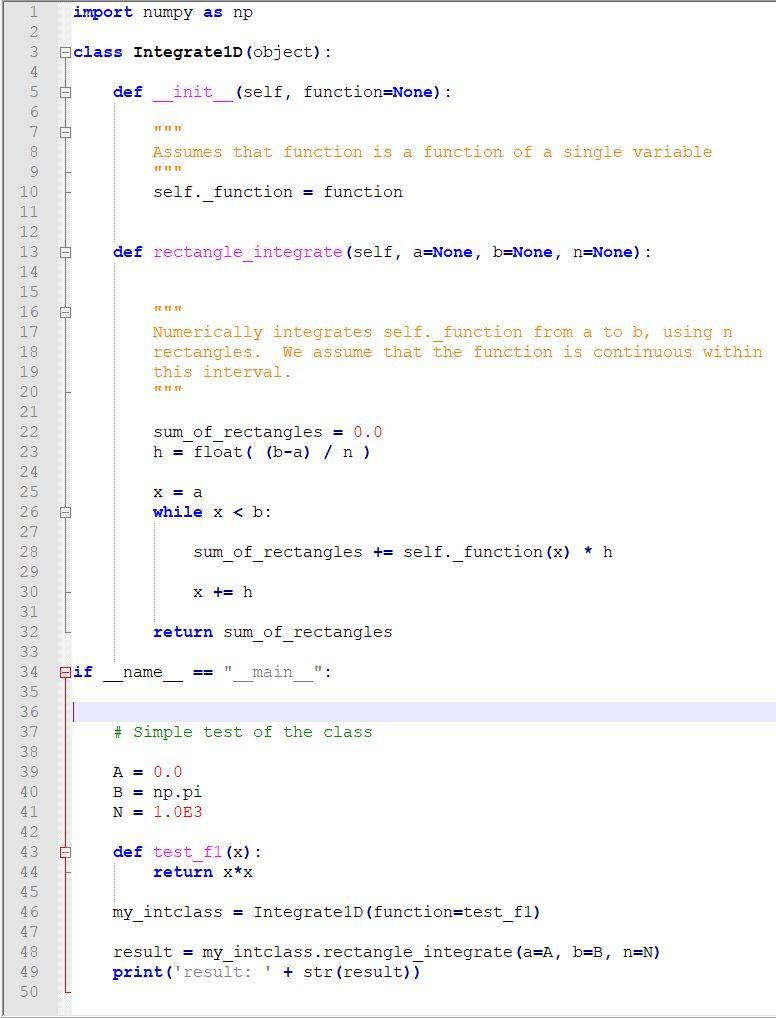
Using the class (attached image), write a Python program that uses this class for experimenting with numerical integration with different step sizes.

Explore and document the effects of using increasing numbers of rectangles to integrate the simple function, over the interval f(x) = x2 x = [1.0, 2.0] . Integrate the function by hand so that you know what the true solution is. Then starting with n = 10 rectangles, you should iterate with increasing numbers of rectangles (increase by a factor of 10 at each iteration) until the absolute value of the difference between the result at the current iteration and the previous iteration is less than a value of ? = 1.0E ? 06 . The output of this program should be a table that shows, for each iteration, the number of rectangles, the width of each rectangle ( h ), the estimated value of the definite integral, and the error (the absolute value of the difference between the current answer and the answer from the previous iteration). There is no need to compare to the true value, because in most interesting cases, you wont know the true value. Your interest here is to know when the solution starts to converge to an acceptable precision. The table should be neatly formatted, with all numbers aligned, looking something like

n h integral error

10 1.0E-1 ????.?E?? ????.?E?? 100 1.0E-2 ????.?E?? ????.?E?? . . . . . . . . . . . .

While you are iterating, you should save the values of h and the error in lists or arrays so that you can create a pyplot plot of error vs h . The x axis ( h ) should be logarithmic, and you can use your judgement about whether the y axis ( error ) should also be logarithmic. Be sure to label the axes meaningfully, and to include a meaningful title.

1 2 3 import numpy as np class Integrate 1D (object): def init (self, function-N ne ) : IT IT Assumes that function is a function of a single variable IT IT 1 10 self. functionfunction 12 13 14 15 16 17 18 19 20 21 def rectangle_integrate (self, a None, b None, n None): Numerically integrates self._function from a to b, using n rectangles. We assume that the function is continuous within this interval It IT IT sum of rectangles 0.0 h= float( (b-a) / n ) 23 24 25 26 27 28 29 30 31 32 while x