Using the given background information, fill out the graph. No more additional information was given. Thank You.

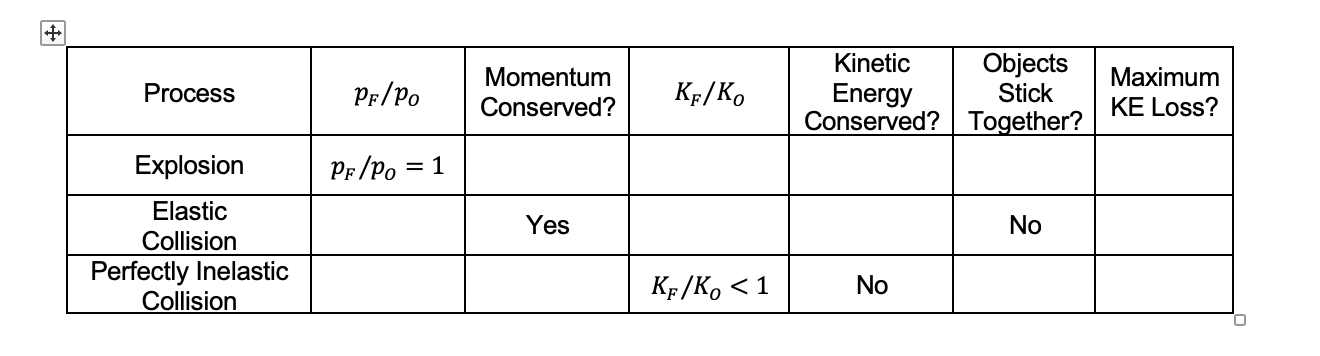
Conservation of Momentum The collision of two carts on a track can be described in terms of momentum conservation and, in some cases, energy conservation. If there is no net external force experienced by the system of two carts, then we expect the total momentum of the system to be conserved. The conservation of momentum can be easily proven mathematically. You just need to remember that the force is the rate at which momentum is supplied (or removed) from a system. So, if the force is zero: 13'" = m& = mA5 = A = 0 At At then: A=0 or, rearranging this: 130 = F Therefore, conservation of momentum can be summarized as: .5 fF =0,then4 = .- (Conservation of Momentum) It might strike you as odd that the net force during a collision is zero. After all, the carts are colliding with one another. If you take the carts individually, there is a net force acting on one cart alone. However, if you take the two carts together as a unit, Newton's 3rd Law ensures that the forces between the carts are equal and opposite and therefore cancel out, leaving no net force. Consequently, momentum will be conserved for the two carts together, but not for either one individually. This is true regardless of the exact nature of the force acting between the carts. In contrast, energy is only conserved when certain types of forces are exerted between the carts. Collisions and Explosions Collisions are classied as: 0 Elastic: Kinetic energy is conserved I Inelastic: Kinetic energy is lost 0 Perfectly Inelastic: The objects stick together after collision with the maximum possible kinetic energy loss 0 Explosive: Kinetic energy is gained In all cases (explosive, elastic, inelastic, and perfectly inelastic), momentum must be conserved. Again, Newton's 31'd Law (i.e. the forces acting between pairs of objects are equal in magnitude and opposite in direction) guarantees this. In this experiment you can observe these types of collisions and test for the conservation of momentum and energy in each case. \f