Question: Using the P(x) = 0.90 P(y) = 0.05 P(z|x,y) = 0.25 P(z|x, y)=0.85 P(z|-x,y) = 0.85 P(z|-x, y)=0.85 What is the probability of P(-x|z)?

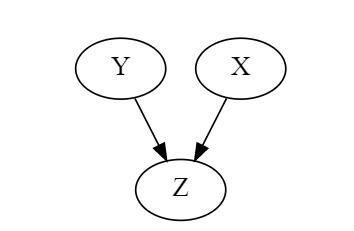
Using the P(x) = 0.90 P(y) = 0.05 P(z|x,y) = 0.25 P(z|x, y)=0.85 P(z|-x,y) = 0.85 P(z|-x, y)=0.85 What is the Y Z X

Using the P(x) = 0.90 P(y) = 0.05 P(z|x,y) = 0.25 P(z|x, y)=0.85 P(z|-x,y) = 0.85 P(z|-x, y)=0.85 What is the probability of P(-x|z)? Bayesian network with the following conditional probability Activ Go to Y Z X

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The problem presented is a classic example of Bayesian inference and we want to calculate the probab... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Q:

What 3 strategies can most affect rapidgrowth in an entrepreneurial venture? Explain your reasoning. What 3 traits of an entrepreneurcan most positively affect entrepreneurial growth? Explain your...

Q:

Consider a binomial distribution with n = 5 trials. Use the probabilities given in Table 2 of the Appendix to make histograms showing the probabilities of r = 0, 1, 2, 3, 4, and 5 successes for each...

Q:

The operation of arc reversal ARC REVERSAL in a Bayesian network allows us to change the direction of an arc X Y while preserving the joint probability distribution that the network represents...

Q:

Help me answer all of the following activities and please do follow the page numberings thank you in advance Activity 3. Direction: Read and analyze the situation below. Answer the questions as...

Q:

Algorithms in Artificial Intelligence (or, the old name: Introduction to Algorithmic Decision Making) Part 1 Based on slides by David Sarne and Lirong Xia Course Tentative Schedule Introduction...

Q:

LAB ACTIVITY #3 For each part of this lab, SUBMIT your solution to everything asked in BOLD RED in Problems 1-6 below. Include the respective R code and output. Part 1 (Continuous Distributions in R)...

Q:

CS 188 Introduction to Fall 2015 Articial Intelligence HW8 INSTRUCTIONS Due: Wednesday, November 4, 2015 11:59 PM Policy: Can be solved in groups (acknowledge collaborators) but must be written up...

Q:

The accompanying table displays finishing times, in seconds, for the winners of fourteen 1-mile thoroughbred horse races. Complete parts (a) through (c) below. Click here to view the finishing times....

Q:

DSCI 2710 PRACTICE EXAM 2-A 1. One of the following statements is false and the other four are true. Identify the false statement. a. For two events, A and B, P(A and B) is equal to P(A)AP(B)...

Q:

An Analysis of the spread Coronavirus (COVID-19) Pandemic across countries Compilation of the COVID-19 epidemic data commenced on the 31st of December 2019. First identified in Wuhan, China, and by...

Q:

The compound K 2 O 2 also exists. A chemist can determine the mass of K in a sample of known mass that consists of either pure K 2 O or pure K 2 O 2 . From this information, can the chemist answer...

Q:

Write an algorithm that accurately computes the roots of a quadratic equation even in situations when subtractive cancellation may severely corrupt the results, i.e. |b| = Vb2 4ac. Convert the...

Q:

1. A robust control system exhibits the desired performance in the presence of significant plant uncertainty. True or False

Q:

What is the mass percent of an aqueous sodium hydroxide solution in 1000 g of H,O if the molality of NaOH is 10.7m?

Q:

Who were the Redeemers in the segregated south, and what was their underlying mission? How did they impact education in the new public schools, and how did they address the issue of free labor...

Q:

_____________ maintenance reporting model, in here maintenance reports to a plant or facilities manager at the same level as production and engineering. This model provides a balanced approach, with...

Q:

Calculate I1, I2, and I3.

Q:

Suppose 12 charged particles of identical charge q are placed around the circumference of a clock of radius r, one at each number positions uniformly separated. (a) Derive the equation for net...

Q:

how to write a project management assignment based on obtaining a qualification? starting with a business case for obtaining a qualification i.e. postgrad

Q:

Effect of Helium-Neon Laser Auriculotherapy on Experimental Pain Threshold is the title of an article in the journal Physical Therapy. In this article, laser therapy is discussed as a useful...

Q:

Numbers are often assigned to data that are categorical in nature. (a) Consider these number assignments for category items describing electronic ways of expressing personal opinions: 1 = Twitter; 2...

Q:

Over the past several months, an adult patient has been treated for tetany (severe muscle spasms). This condition is associated with an average total calcium level below 6 mg/dL. Recently, the...

Q:

At issue is the proportion of people in a particular county who do not have health care insurance coverage. A simple random sample of 240 people was asked if they have insurance coverage, and 66...

Q:

A random sample of 200 items reveals that 144 of the items have the attribute of interest. a. What is the point estimate for the population proportion for all items having this attribute? b. Use the...

Q:

A decision maker is interested in estimating a population proportion. A sample of size n = 150 yields 115 successes. Based on these sample data, construct a 90% confidence interval estimate for the...