Using the references below please answer the advanced geometry problem:

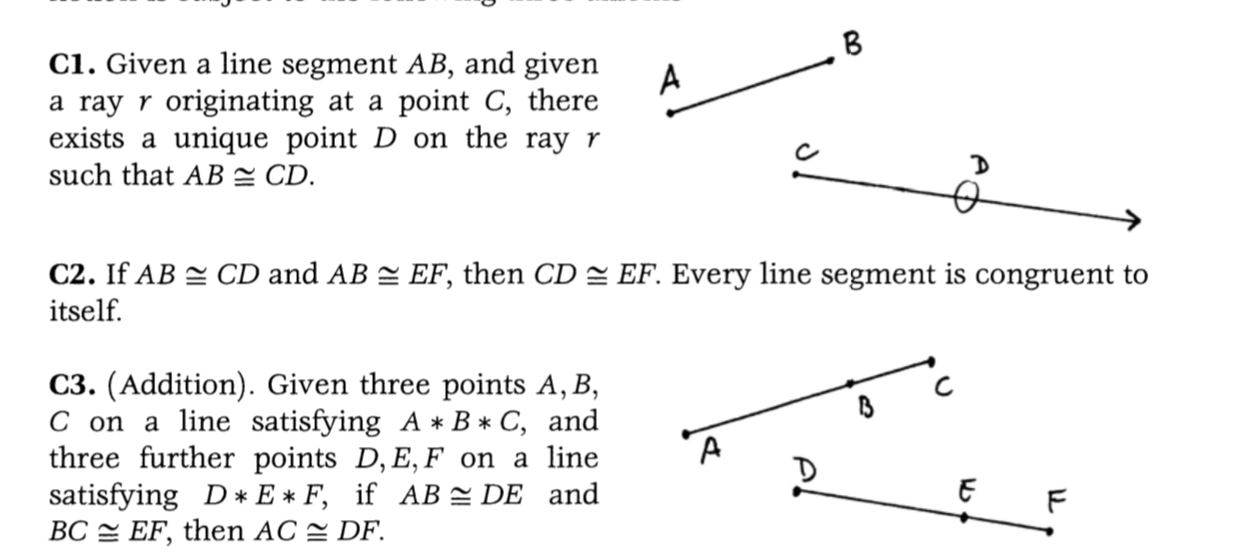
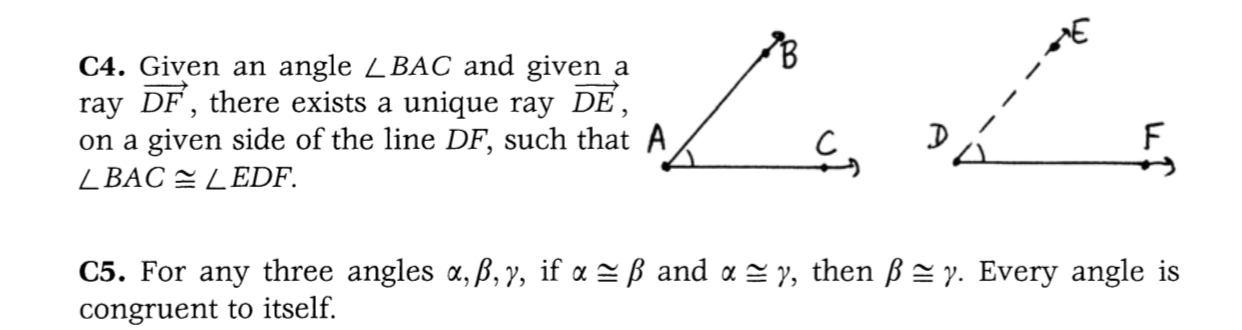
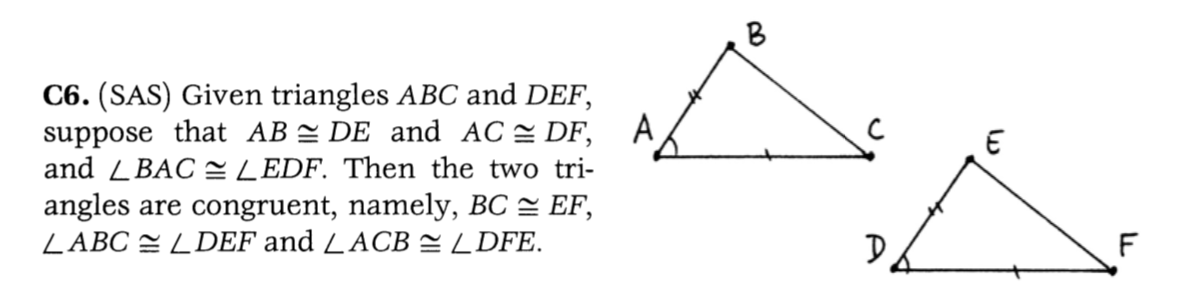
C1. Given a line segment AB, and given a ray r originating at a point C, there A exists a unique point D on the ray r such that AB ~ CD. C D C2. If AB ~ CD and AB ~ EF, then CD ~ EF. Every line segment is congruent to itself. C3. (Addition). Given three points A, B, C C on a line satisfying A * B * C, and B three further points D, E, F on a line A satisfying D * E *F, if AB ~DE and D E F BC ~ EF, then AC ~ DF.C4. Given an angle ZBAC and given a B ray DF, there exists a unique ray DE, on a given side of the line DF, such that A LBAC ~ LEDF. C D C5. For any three angles a, B, y, if a ~ B and a ~ y, then B ~ y. Every angle is congruent to itself.\f8.7 Consider the real Cartesian plane IR, with lines and betweenness as before (Exam- ple 7.3.1), but define a different notion of congruence of line segments using the distance function given by the sum of the absolute values: d(A, B) = la1 - bil + laz - b2l, where A = (a1, a2) and B = (b1, b2). Some people call this "taxicab geometry" be- cause it is similar to the distance by taxi from one point to another in a city where all streets run east-west or north-south. Show that the axioms (Cl), (C2), (C3) hold, so that this is another model of the axioms introduced so far. What does the circle with center (0, 0) and radius 1 look like in this model?9.3 Consider the real Cartesian plane where congruence of line segments is given by the absolute value distance function (Exercise 8.7). Using the usual congruence of angles that you know from analytic geometry (Section 16), show that (C4) and (CS) hold in this model, but that (C6) fails. (Give a counterexample.) 1. Consider the Taxicab Model on R? as defined in class. (See exercises 8.7 & 9.3) (a) Given AB, where A = (1, 0) and B = (2, -1). and ray T, where the ray is given by y = x for x 2 0 (origin point C = (0, 0)). Copy AB to T' by finding point D such that CD ~ AB. (b) Find 3 different triangles in the model: one equilateral, one isosceles, and one scalene. (c) Consider the triangle AABC, where A = (0,0), B = (2,0), and C = (0,1). Find a different triangle in the model that is congruent to AABC. (d) Draw the unit circle in this model. Be sure to label everything appropriately. (e) Show that the congruence axiom (C1) holds in this model. (f) Show that the congruence axiom (C2) holds in this model. (g) Show that the congruence axiom (C3) holds in this model. (h) Show that the congruence axiom (C6) fails in this model by giving a counter-example