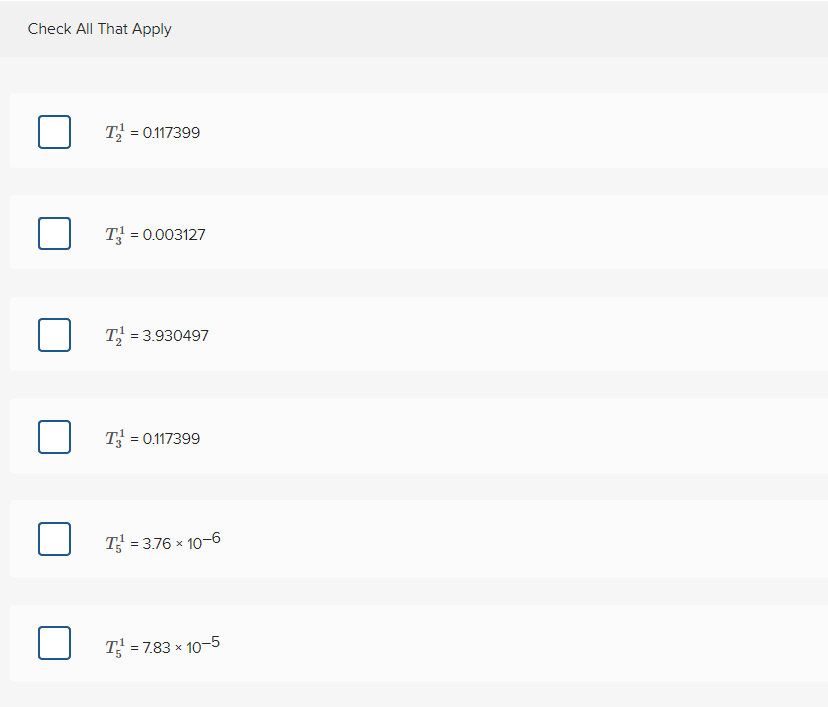
Using the simple implicit finite-difference approximation, solve for the temperature distribution of a long, thin rod with a length of 10 cm and the following values: k'= 0.49 cal/(s - cm - C), Ax= 2 cm, and At= 0.1 s. At t= 0, the temperature of the rod is zero and the boundary conditions are fixed for all times at 7(0) = 100C and 7(10) = 0C. Note that the rod is aluminum with C = 0.2174 cal/g - C) and p= 2.7 g/cm3. Therefore, k= 0.835 cm2/s and 1 = 0.020875. Identify the correct values of T from the following computed at t= 0.1. Here, the derivative at x = 10 is equal to zero. Check All That Apply T, = 0.117399 T:1 = 0.003127 7,1 = 3.930497 T31 = 0.117399 T1 = 3.76 x 10-6 X T= 7.83 x 10-5