) Using the structure of the matrix A and the Gershgorin circle theorem, find the smallest interval containing the eigenvalues of A (without actually computing them here). ii) Compute the eigenvalues of A. Then on the same picture, draw the Gershgorin disks you found in i) and indicate the eigenvalues you just computed. iii) Compute ?A?1, ?A?2, and ?A??. iv) Decompose the matrix as A = Q?QT , where Q is an orthogonal matrix and ? is a diagonal matrix.

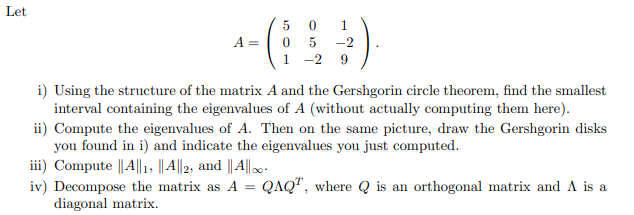
Let 5 l] l A = 5 2 1 2 9 i} Using the structure of the matrix A and the Gershgorin circle theorem1 find the smallest inten'aJ containing the eigenvalues of A [without actually computing them here}. ii} Compute the eigenvalues of A. Then on the same picture, draw the Get'shgot'in disks you [ouncl in i} and indicate the eigenvalues you just computed. iii} Compute ||A||11 ||A||2+ and ||A||w hr} Deoompose the matrix as A : QAQT, where Q is an orthogonal matrix and A is a diagonal matrix