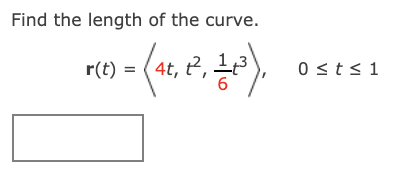
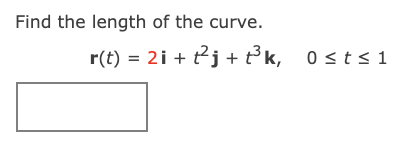
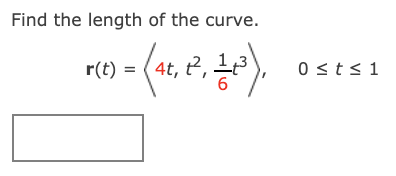
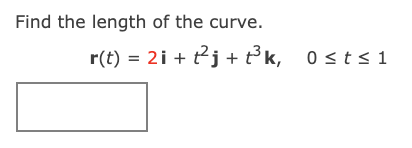
_utorial Exercise Find the length of the curve. r(t) = (3r, 3 cos(t), 3 sin(t)), 9 s t s 9 For r(t) = (f(t), g(t), h(t)), the length of the arc from t = a to t = b is found by the integral L = f \"J (m)2 + (gun'- + (W)? or: = f b mm dt. We, therefore, need to find the components of r'(t). For r(t) = (3:, 3 cos(t), 3 sin(t)), we have Consider the vector function given below. r(t) = (15t, 4 cos(t), 4 sin(t)) Exercise (a) Find the unit tangent and unit normal vectors T(t) and N(t). Step 1 We start by finding the tangent vector to the curve. For r(t) = (15t, 4 cos(t), 4 sin(t)), we have r'(t) =