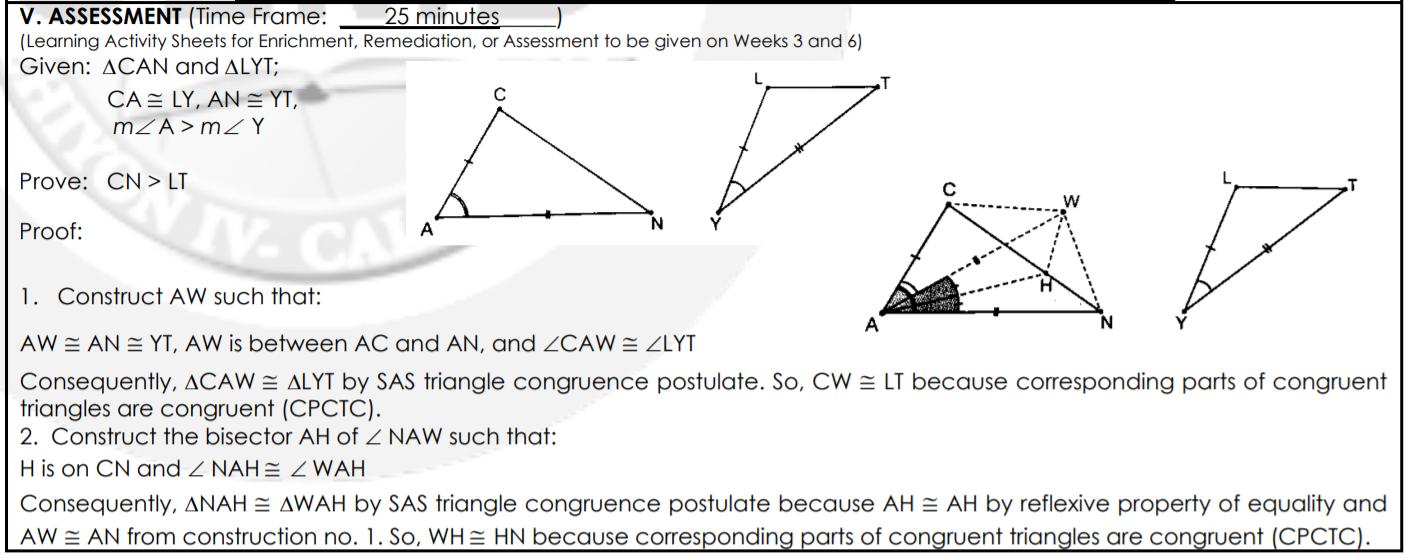
V. ASSESSMENT (Time Frame: 25 minutes (Learning Activity Sheets for Enrichment, Remediation, or Assessment to be given on Weeks 3 and 6) Given: ACAN and ALYT; CA LY, AN=YT, m/A>mZY Prove: CN > LT Proof: IV. CAL 1. Construct AW such that: A L A AW ANYT, AW is between AC and AN, and ZCAW = ZLYT Consequently, ACAW ALYT by SAS triangle congruence postulate. So, CW LT because corresponding parts of congruent triangles are congruent (CPCTC). 2. Construct the bisector AH of Z NAW such that: H is on CN and Z NAHE ZWAH Consequently, ANAHE AWAH by SAS triangle congruence postulate because AH AH by reflexive property of equality and AWAN from construction no. 1. So, WH HN because corresponding parts of congruent triangles are congruent (CPCTC).