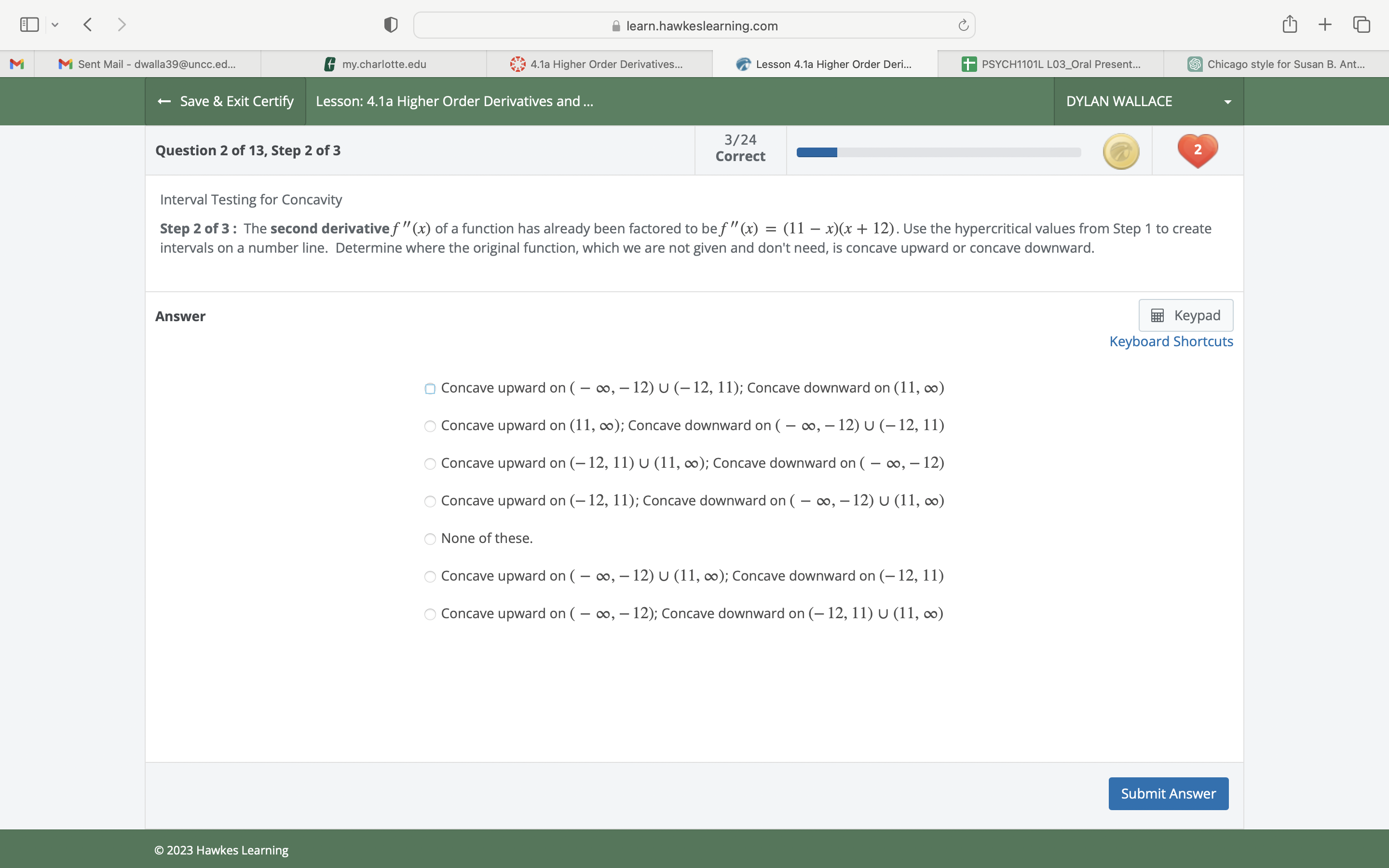
v > learn.hawkeslearning.com C + M M Sent Mail - dwalla39@uncc.ed... my.charlotte.edu 4.1a Higher Order Derivatives... Lesson 4.1a Higher Order Deri... + PSYCH1101L L03_Oral Present.. Chicago style for Susan B. Ant... + Save & Exit Certify Lesson: 4.1a Higher Order Derivatives and ... DYLAN WALLACE 3/24 Question 2 of 13, Step 2 of 3 Correct Interval Testing for Concavity Step 2 of 3: The second derivative f "(x) of a function has already been factored to bef" (x) = (11 - x)(x + 12). Use the hypercritical values from Step 1 to create intervals on a number line. Determine where the original function, which we are not given and don't need, is concave upward or concave downward. Answer Keypad Keyboard Shortcuts D Concave upward on ( - co, - 12) U (-12, 11); Concave downward on (11, co) Concave upward on (1 1, co); Concave downward on ( - co, - 12) U (-12, 11) Concave upward on (- 12, 11) U (11, co); Concave downward on ( - co, - 12) Concave upward on (- 12, 11); Concave downward on ( - co, - 12) U (11, co) None of these. Concave upward on ( - co, - 12) U (11, co); Concave downward on (- 12, 11) O Concave upward on ( - co, - 12); Concave downward on (- 12, 11) U (11, co) Submit Answer 2023 Hawkes Learning