Vector Calculus - Maximums and Minimums

Suppose that f(x,y)f(x,y) = x2?xy+y2?2x+2yx2-xy+y2-2x+2y with:

D={(x,y)?0?x?2,0?y?2}D={(x,y)?0?x?2,0?y?2}.

1)The critical point of f(x,y)f(x,y) on the boundary of DD, not at a corner point, is at (a,b)(a,b). Then a=________

and

b=_______

2) Absolute minimum on the boundary of f(x,y)f(x,y) is = ________

and absolute maximum on the boundary is 8__________

fx = 0, fy= 0

x= 2/3 and y = -2/3

y=0 points are (2,0)

x= 1 points are (1,0)

Images below are hand written content for tutor to review for support.

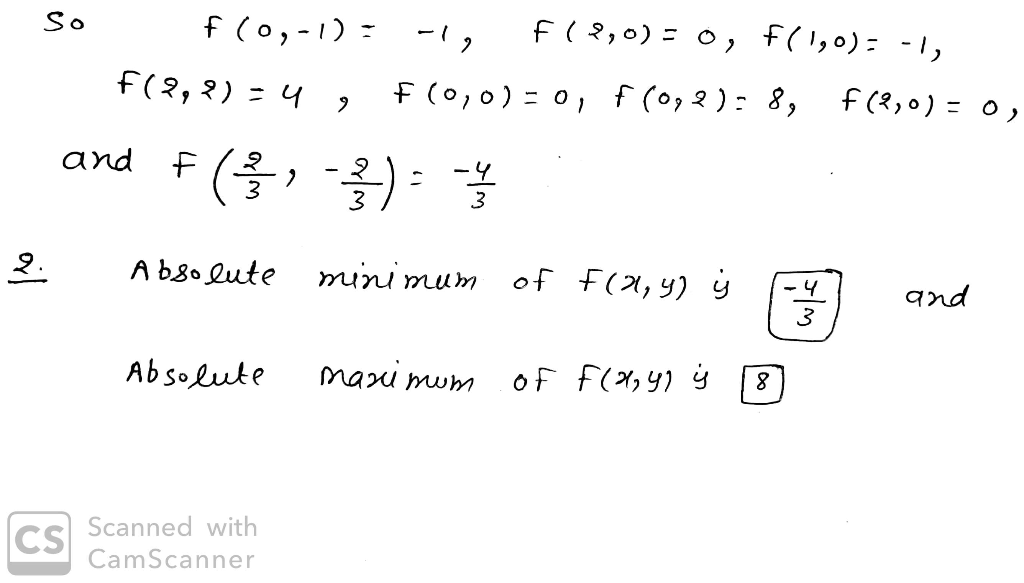
Sop As given F (X, 4) = 207 - 204 + 42 - 9*+ 94 Fx (21, 4 ) = 2x-4- 9 and fy (x , y ) : 24- 2+8 for stationary point, fx = 0 , fy : 0 2X- y :2 and 24-x = - 2 both solving and we get x = 2 and y : -. 3 W A so cutical points are and b = W / AD Now Conner points are (0 , 0), ( 0, 2), ( 9, 0), (2 , 2) Also Find the boundary points- ie. when 2 = 0 the . F ( 0 , 4 ) = 42+24 and fy (0 , 4 1 = 24+2 Set fy : 0 3 24+2=0 0% y = - 1 So B. points are ( 0 ) - 1 ) when * = 2, F ( 2 , 47 : 1212 - 2 4 + 42 - 4 +24 = 42 andfy:2; set fy = 0 => (y=0 So B. points are ( 2, 0 ) when y= 0, F ( 21 , 0 ) = 219- 321 and fx ( 21 10 ) = 2x - 2 and 2X - 2 = 0 (x = 1 So B. points are 1( 1,0 ) when y:2, F ( 21 , 9) : 219 - 2x + 4 - 9 x +4 and fx (2,2): 2x-4 0 22 - 4 : 0 7 21 =2 CS Scanned with CamScanner B. points are (8, 2)So f ( 0 , - 1 ) = - 19 F ( 8, 0 ) = 0, f ( 1,0 ) = -1, F ( 9 , 8 ) = 4 , F ( 0 , 0 ) = 0, f ( 0 , 2 ) : 8, f ( 9, 0 ) = 0, and f 3 -3 ) 3 2 . Absolute minimum of F (21, 4 ) y and Absolute maximum OF F (x, 4) is 8 CS Scanned with CamScanner