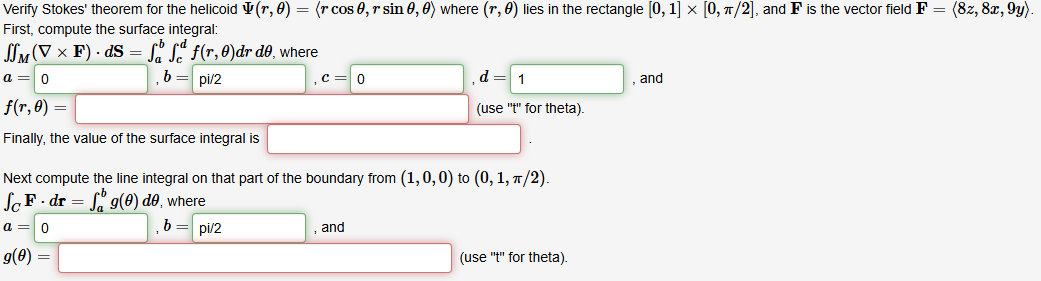
Question: Verify Stokes' theorem for the helicoid Psi ( r , theta ) = ( :rcos theta , rsin theta ,
Verify Stokes' theorem for the helicoid Psi rtheta :rcostheta rsintheta theta :) where rtheta lies in the rectangle times pi and F is the vector field F:zxy:
First, compute the surface integral:
Mgradtimes FdSintab intcd frtheta drdtheta where
a
b
c
d
and
frtheta
use t for theta
Finally, the value of the surface integral is
Next compute the line integral on that part of the boundary from to pi
intC Fdrintab gtheta dtheta where
a
b
and
gtheta
use t for theta
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


