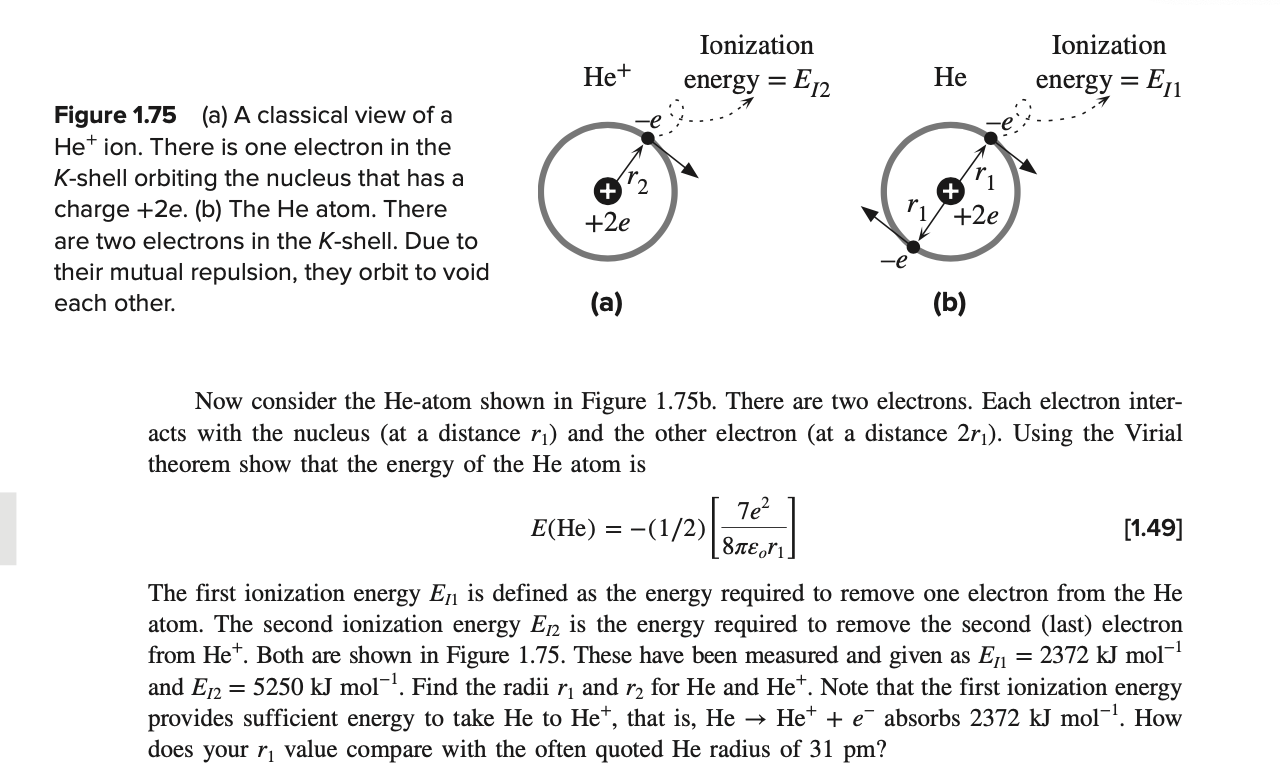
Virial theorem and the He atom In Example 1.1, we calculated the radius of the H-atom using the Virial theorem. First consider the Het atom, which as shown in Figure 1.75a has one electron in the K-sell orbiting the nucleus. Take the PE and the KE as zero when the electrons and the nucleus are infinitely separated. The nucleus has a charge of +2e and there is one electron orbiting the nucleus at a radius r2. Using the Virial theorem show that the energy of the Het ion is 2e2 E(He+) = -(1/2) = [1.48] 4 r2 He+ Ionization energy = E12 Ionization energy = E11 = He = Figure 1.75 (a) A classical view of a Het ion. There is one electron in the K-shell orbiting the nucleus that has a charge +2e. (b) The He atom. There are two electrons in the K-shell. Due to their mutual repulsion, they orbit to void each other. ri +2e +2e -e (a) (b) Now consider the He-atom shown in Figure 1.75b. There are two electrons. Each electron inter- acts with the nucleus (at a distance r) and the other electron (at a distance 2r). Using the Virial theorem show that the energy of the He atom is 7e? E(He) = -(1/2) [1.49] 81,ri. = The first ionization energy Eji is defined as the energy required to remove one electron from the He atom. The second ionization energy E12 is the energy required to remove the second (last) electron from Het. Both are shown in Figure 1.75. These have been measured and given as En = 2372 kJ mol-? and E12 = 5250 kJ mol-!. Find the radii r and r2 for He and He+. Note that the first ionization energy provides sufficient energy to take He to He+, that is, He Het + absorbs 2372 kJ mol-?. How does your r value compare with the often quoted He radius of 31 pm