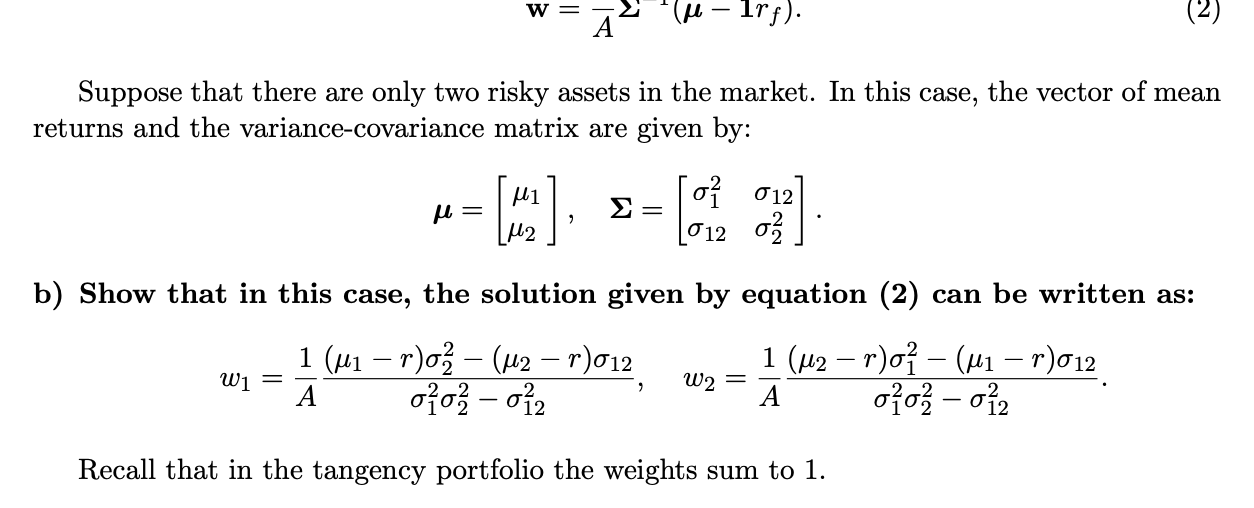
W = (u - Irf). (2) Suppose that there are only two risky assets in the market. In this case, the vector of mean returns and the variance-covariance matrix are given by: o 012 = = leny (012 o b) Show that in this case, the solution given by equation (2) can be written as: W1 = 1 (M1 r)o (u2 r)012 g?i - P2 W2 = 1 (u2 r)o (ui r)012 A oo-012 Recall that in the tangency portfolio the weights sum to 1. W = (u - Irf). (2) Suppose that there are only two risky assets in the market. In this case, the vector of mean returns and the variance-covariance matrix are given by: o 012 = = leny (012 o b) Show that in this case, the solution given by equation (2) can be written as: W1 = 1 (M1 r)o (u2 r)012 g?i - P2 W2 = 1 (u2 r)o (ui r)012 A oo-012 Recall that in the tangency portfolio the weights sum to 1