Question: We are given a directed graph G = (V, E) , where V = {1, ... n} , i.e. the vertices are integers in the

We are given a directed graph G = (V, E) , where V = {1, ... n} , i.e. the vertices are integers in the range 1 to n. For every vertex 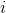we would like to compute the values 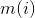defined as follows: 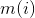is the smallest 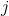compute the values defined as follows: is the smallest such that vertex such that vertex 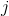is reachable from vertex 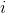(As a convention, we assume that 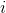is reachable is re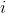achable from vertex from .) Show that the values can be computed in time. (As a convention, we assume that image text in transcribed is reachable from .) Show that the values 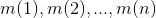can be computed in 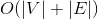time.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Given a directed graph G = (V, E) and a pair of vertices s, t in G, the Hamiltonian Path problem asks whether there is a simple path from s to t that visits every vertex of G exactly once. The...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

(iii) Now express your decision rule instead using only the quantities p(Ck), p(Cj ), p(x|Ck), p(x|Cj ), and relate it to the diagram above. [2 marks] (iv) If the classifier decision rule assigns...

Dijkstras algorithm is a greedy algorithm for solving single-source shortest-paths problems on a graph in which all edge weights are non-negative. Study the introductory section and Dijkstras...

Give the typing rules for Peano natural numbers and their eliminator.(ii) Using the rules given above, define the addition function.] (iii) Let a binary tree be either a leaf Leaf or a node...

1 Removing Train Stations (50 points) = 2 We discussed in class how one of the original motivations for studying max-flow and min-cut comes from WWII, and in particular the questions of how much...

Describe an algorithm to generate G2 from G1. [12 marks] How could this algorithm be used to generate the transitive closure of a graph given its adjacency matrix? [5 marks] What is the cost of this...

4. Collaborative: We define the Escape Problem as follows. We are given a directed graph G V, E) (picture a network of roads.) A certain collection of vertices X C V are designated as populated...

Clin Corporation haa an overhead crane that has an estimated remaining life of 10 years. The crane can be sold now for 800,000. If the crane is kept in service, it must be overhauled immediately at...

Why is it so difficult to find unknown interest or growth rates and numbers of periods when all other variables are known? When must you use trial-and-error techniques?

Jensen Shipping currently has an EPS of $ 2 . 3 1 , a benchmark PE of 1 3 . 5 , and an earnings growth rate of 2 . 3 percent. What is the target share price 4 years from now?

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

4. Describe how much money is spent on training in U.S. companies and how the money is used.

2. Discuss various aspects of the training design process.

3. Describe the amount and types of training occurring in U.S. companies.