We are given six matrices A1, A2, A3, A4, A5 and A6 for which we wish to compute the product A = A1 A2 A3 A4 A5 A6 where Ai is a di1 di matrix. Since matrix multiplication is associative we can parenthesise the expression for A any way we wish and we will end up with the same result. What is the minimum number of scalar multiplications we have to perform if d0 = 3, d1 = 4, d2 = 5, d3 = 6, d4 = 5, d5 = 3 and d6 = 2? How do we parenthesise the expression for A to achieve this number? Present your partial results in a table.

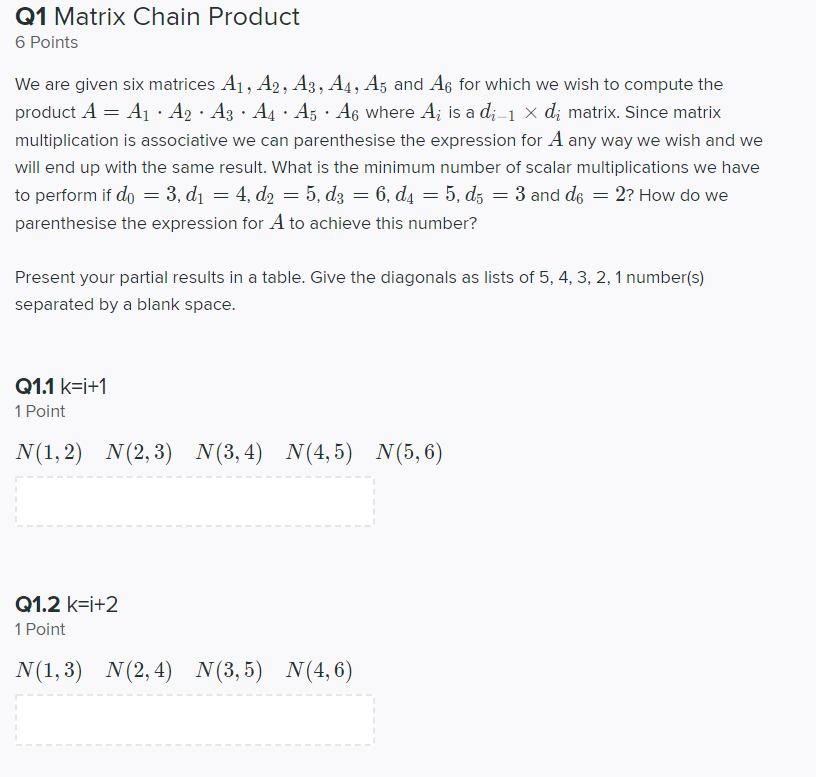
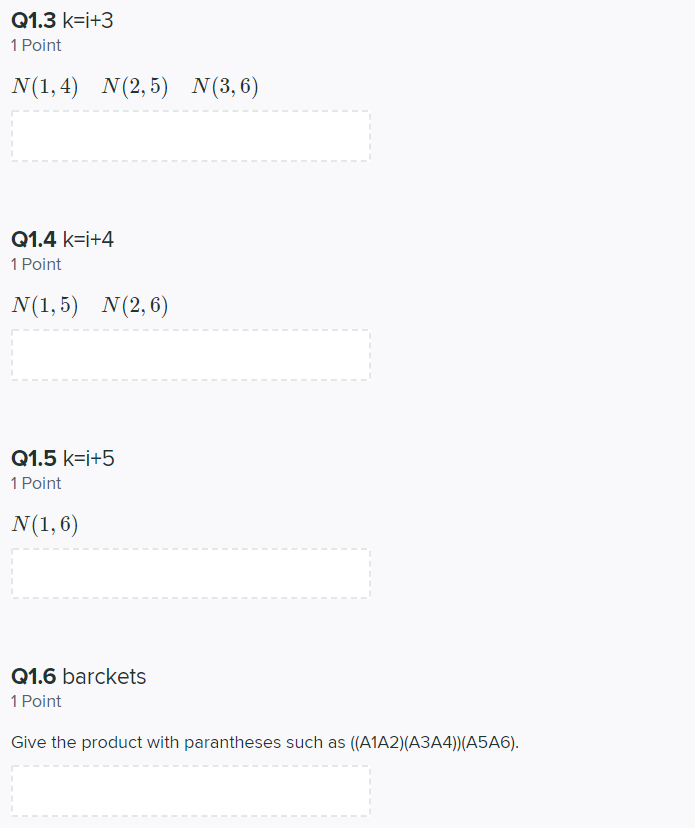
Q1 Matrix Chain Product 6 Points We are given six matrices A1, A2, A3, A4, A5 and A6 for which we wish to compute the product A = A1 A2 A3 44 Az A6 where A; is a di1 x di matrix. Since matrix multiplication is associative we can parenthesise the expression for A any way we wish and we will end up with the same result. What is the minimum number of scalar multiplications we have to perform if do = 3, dj = 4, d2 = 5, d3 = 6, d4 = 5, d5 = 3 and do = 2? How do we parenthesise the expression for A to achieve this number? Present your partial results in a table. Give the diagonals as lists of 5, 4, 3, 2, 1 number(s) separated by a blank space. Q1.1 k=i+1 1 Point N(1,2) N(2,3) N(3,4) N(4,5) N(5,6) Q1.2 k=i+2 1 Point N(1,3) N(2,4) N(3,5) N(4,6) Q1.3 k=i+3 1 Point N(1,4) N(2,5) N(3,6) Q1.4 k=i+4 1 Point N(1,5) N(2,6) Q1.5 k=i+5 1 Point N(1,6) Q1.6 barckets 1 Point Give the product with parantheses such as ((A1A2)(A3A4))(A5A6)