Question: We are given the following third - order homogeneous differential equation. y ' ' ' 1 2 y ' ' 3 6 y ' =
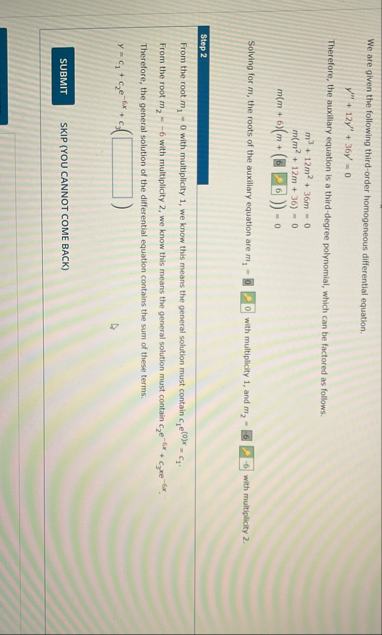
We are given the following thirdorder homogeneous differential equation.
Therefore, the auxiliary equation is a thirddegree polynomial, which can be factored as follows.
Solving for the roots of the auxiliary equation are with multiplicity and with multiplicity
Step
From the root with multiplicity we know this means the general solution must contain
From the root with multiplicity we know this means the general solution must contain
Therefore, the general solution of the differential equation contains the sum of these terms.
SKIP YOU CANNOT COME BACK
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


