We are given two numbers b , c such that c divides b i.e. c | b and b , c 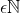. Then b = c * L where L .

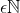b is NOT a prime number.

There is a Statement S(m): We are given a sequence of numbers 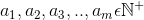as long as b divides 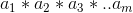, it follows that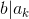

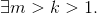
Question: Please identify and write about where the proof given below fails :

We assume that by strong induction on m, statement S(m) given a sequence of numbers 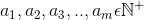as long as b divides 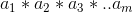, it follows that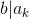

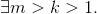
given b is prime.

Next step is to show S(m) is true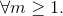

Next step is to assume m= 1 and thus 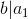for k = 1which means b divides .

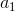Next step is to let S( L ) be true 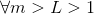hence we show in the next step S(m + 1 ) .

To demonstrate S(m + 1 ) , let 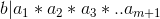which means b can divide them. We prove 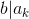given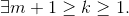

Next step is to define 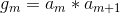such that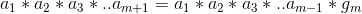

Next step 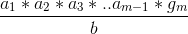where sequence of m terms is divisible by b .

So using mathematical technique of induction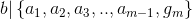

Next step --> First Scenario: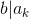

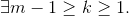
ELSE Next step --> Second Scenario: .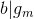

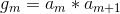
Thus proving that if 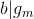it can divide both terms comprising 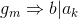such that 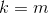or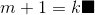

What is wrong with this proof ? Help is appreciated!

01, 02, 03, .., am EN+ d1 * 2 * d3 * ..am bak Em >k> WA 1. k> 1. 9m am * am+1 d1 * 2 * d3 * ..adm+1 = d1 * 2 * d3 * ..am-1 * 9m aj * a2 * a3 *..am-1 * 9m b bl{a1, 42, 43, .., am-1,9m Em - 1 >k > 1. b 9m 9m blak k=m m+1=k