we considered the situation where we have a box

containing an unknown number?say N?of identical bolts. In order to get an

idea of the size of N we introduced three random variables X, Y , and Z. Here

we will use X and Y , and in the next exercise Z, to find maximum likelihood

estimates of N.

a. Suppose that x1, x2,...,xn is a dataset, which is a realization of a random

sample from a Geo(1/N) distribution. Determine the maximum likelihood

estimate for N.

b. Suppose that y1, y2,...,yn is a dataset, which is a realization of a random

sample from a discrete uniform distribution on 1, 2,...,N. Determine the

maximum likelihood estimate for N.

21.12 (Exercise 21.11 continued.) Suppose that m bolts in the box were

marked and then r bolts were selected from the box; Z is the number of

marked bolts in the sample. (Recall that it was shown in Exercise 4.13 c that

Z has a hypergeometric distribution, with parameters m, N, and r.) Suppose

that k bolts in the sample were marked. Show that the likelihood L(N) is

given by

L(N) =

m

k

N?m

r?k

N

r

.

Next show that L(N) increases for N mr/k,

and conclude that mr/k is the maximum likelihood estimate for N.

(a) Fred visits Blotchville again. He finds that the city has installed an electronic display

at the bus stop, showing the time when the previous bus arrived. The times between

arrivals of buses are still independent Exponentials with mean 10 minutes. Fred waits

for the next bus, and then records the time between that bus and the previous bus. On

average, what length of time between buses does he see?

(b) Fred then visits Blunderville, where the times between buses are also 10 minutes on

average, and independent. Yet to his dismay, he finds that on average he has to wait more

than 1 hour for the next bus when he arrives at the bus stop! How is it possible that the

average Fred-to-bus time is greater than the average bus-to-bus time even though Fred

arrives at some time between two bus arrivals? Explain this intuitively, and construct a

specific discrete distribution for the times between buses showing that this is possible.

43. Fred and Gretchen are waiting at a bus stop in Blotchville. Two bus routes, Route 1

and Route 2, have buses that stop at this bus stop. For Route i, buses arrive according

to a Poisson process with rate.

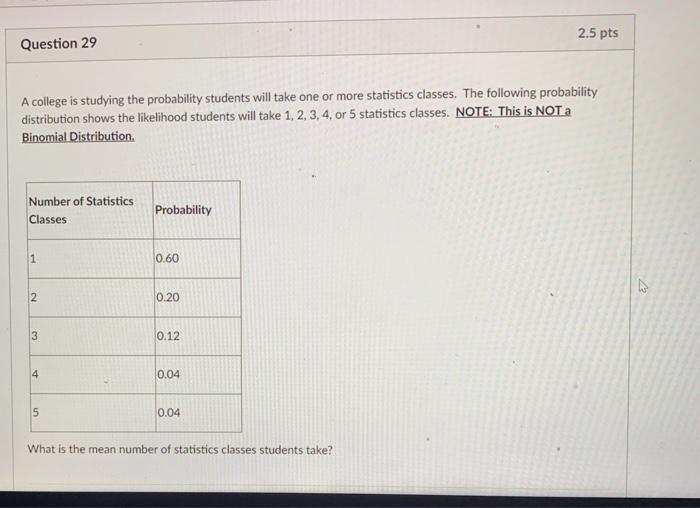
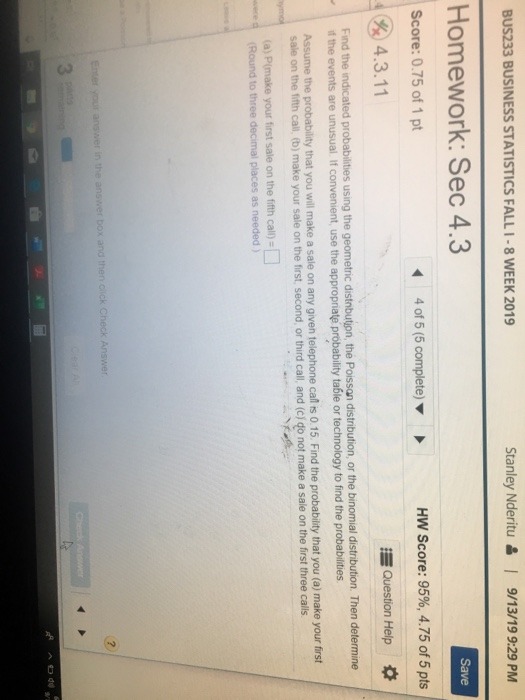
Question 29 2.5 pts A college is studying the probability students will take one or more statistics classes. The following probability distribution shows the likelihood students will take 1, 2, 3, 4, or 5 statistics classes. NOTE: This is NOT a Binomial Distribution. Number of Statistics Classes Probability 1 0.60 2 0.20 3 0.12 4 0.04 5 0.04 What is the mean number of statistics classes students take?BUS233 BUSINESS STATISTICS FALL I - 8 WEEK 2019 Stanley Nderitu & | 9/13/19 9:29 PM Homework: Sec 4.3 Save Score: 0.75 of 1 pt 4 of 5 (5 complete) HW Score: 95%, 4.75 of 5 pts 4.3.11 Question Help Find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine if the events are unusual. If convenient, use the appropriate probability table or technology to find the probabilities. Assume the probability that you will make a sale on any given telephone call is 0.15. Find the probability that you (a) make your first sale on the fifth call, (b) make your sale on the first, second, or third call, and (c) do not make a sale on the first three calls. (a) P(make your first sale on the fifth call) = (Round to three decimal places as needed.) Enter your answer in the answer box and then click Check Answer.Question 3. [This question is based on Problem 43, p. 116 in the textbook] (a) Let {A1,A2} be a partition of a sample space and let B be any event. State and prove the Law of Total Probability as it applies to the partition {A1, A2} and the event B. There are two coins in a box; one coin is a fair coin, and the other is a biased coin that comes up heads 75 percent of the time. Fiona chooses a coin at random and tosses it. (b) What is the probability that the chosen coin ips heads? (Hint: The Law of Total Probability.) (c) Given that the chosen coin ips heads, what is the conditional probability that it was the biased coin? (Hint: Bayes' Theorem.) (d) Given that the chosen coin ips tails, what is the conditional probability that it was the biased coin