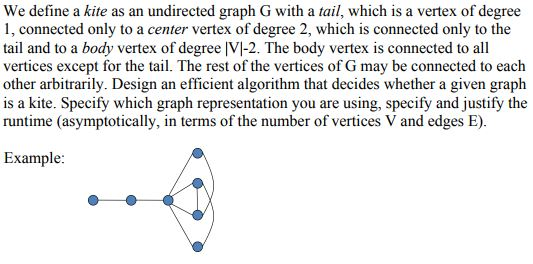
We define a kite as an undirected graph G with a tail, which is a vertex of degree 1, connected only to a center vertex of degree 2, which is connected only to the tail and to a body vertex of degree IVI-2. The body vertex is connected to all vertices except for the tail. The rest of the vertices of G may be connected to each other arbitrarily. Design an efficient algorithm that decides whether a given graph is a kite. Specify which graph representation you are using, specify and justify the runtime (asymptotically, in terms of the number of vertices V and edges E) Example We define a kite as an undirected graph G with a tail, which is a vertex of degree 1, connected only to a center vertex of degree 2, which is connected only to the tail and to a body vertex of degree IVI-2. The body vertex is connected to all vertices except for the tail. The rest of the vertices of G may be connected to each other arbitrarily. Design an efficient algorithm that decides whether a given graph is a kite. Specify which graph representation you are using, specify and justify the runtime (asymptotically, in terms of the number of vertices V and edges E) Example