1. We established the log_t((n+1)/2) upper bound on the height of B-trees of minimum degree t. Derive a lower bound on the height of B-trees of minimum degree t; justify your answer. Compute the values of your lower-bound formula for t = 100, n = 10⁶, 10⁹, 10¹², 10¹⁵; show the values to two decimal places.
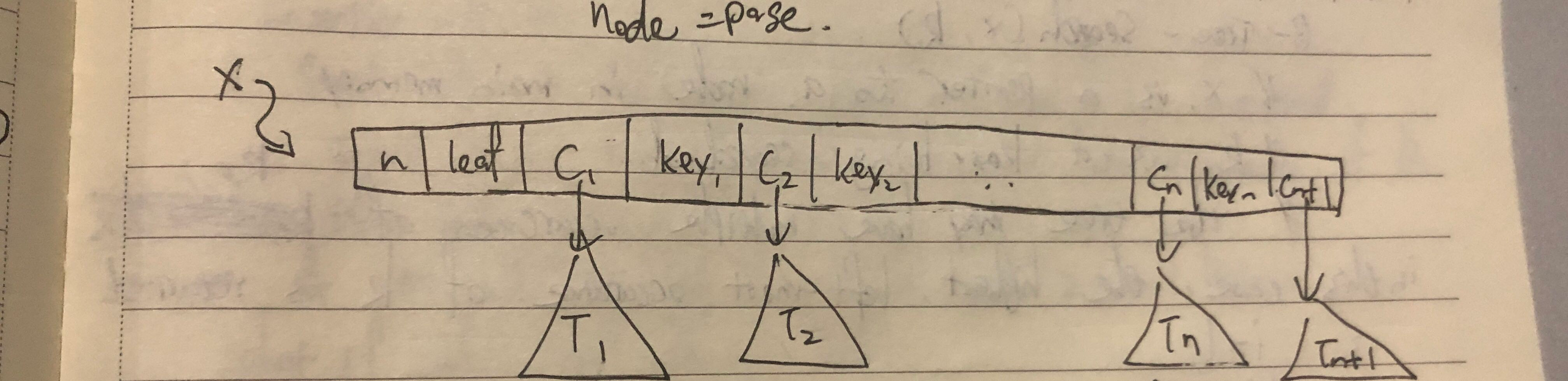
2. Write pseudocode for each of the following B-tree functions. Analyze their runtime efficiency in terms of the # of page reads performed and express it in asymptotic O(f(n)) notation where n is the # of keys in the tree whose root is pointed to by x. Describe your analysis.
   1. Min(x) // Returns the minimum key value in the B-tree whose root is pointed to by x.
   2. Max(x) // Returns the maximum key value in the B-tree whose root is pointed to by x.
   3. height(x) // Returns the height of the B-tree whose root is pointed to by x.
   4. countNodes(x) // Returns the total # of nodes in the B-tree whose root is pointed to by x.
   5. countKeys(x) // Returns the total # of keys in the B-tree whose root is pointed to by x.

B-tree function