Question: We knew that (V, W) is a vector space. Suppose that X is a subset of V (X may or may not be a subspace).

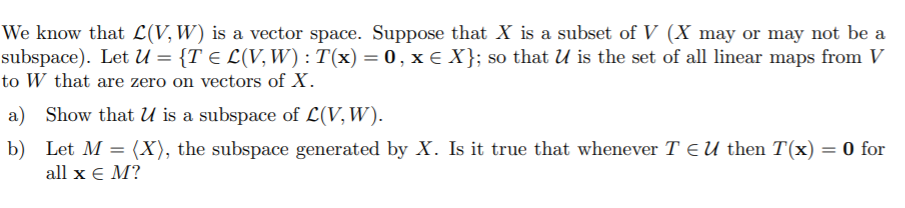
We knew that (V, W) is a vector space. Suppose that X is a subset of V (X may or may not be a subspace). Let U = {T E 130/, W) :T(x) = 0 , x E X}; so that U is the set ofall linear maps from V to W that are zero on vectors of X. a) Show that Ll is a subspace of (V, W). b) Let M = (X ), the subspace generated by X. Is it true that Whenever T E U then T(x) = I] for all x E M '

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

We know that (V, W) is a vector space. Suppose that X is a subset of V (X may or may not be a subspace). Let L! = {T E (V, W) : T(x) = 0, x E X}; so that U is the set of all linear maps from V to W...

LetVandWbe arbitrary subspaces ofRn. We define thesumofVandWto be the set V+W={?v+w?|?v?Vandw??W}.We define theproductofVandWto be the set VW={(?v,w?)|?v?Vandw??W}. It is not hard to check1that the...

Suppose U = {(x, x, y, y) = F4 : x, y = F}. Find a subspace W of F such that F = U W. CHAPTER 1 Vector Spaces Suppose U = {(x, y, x+y.x-y, 2x) e FS: x, y = F}. Find a subspace W of F5 such that F5 =...

MAT 211 Assessment Revised 20WN For the given transformation, find the standard matrix A to represent the transformation in the form U - AU. X X T: R' - R' given by H y x+y Select one: O a. 1 0 0 O...

1. Let V be the real vector space of 3 x 3 symmetric matrices. A typical element of V looks like a d d b e f for some a, b, c, d, e, f E R. Let W be the real vector space of degree 3 polynomials in...

Let V be a vector space over a field F. Let 0 E V denote its zero vector and let x E V be an arbitrary vector. a) Suppose F = R. Prove the following statement: Let V be a vector space over R. Then x...

(a) Find the transition matrix S from B' to B. (b) Use the matrices S and A to find [v], and [T(v)], where [V]B/ = (-1,4) T. (c) Find S" and A' (the matrix for T relative to B' ). (d) Find [T(v)]B,...

4. Let hom(V, W) denote the space of all linear transformations from V to W. Suppose that dim V = n, dim W = m. Prove that hom (V, W) is a vector space (you just need to define notions of addition...

Let V = P(R) be the vector space of polynomials with coefficients in R and let X be a finite subset of V. Prove that there exists an element of V which cannot be expressed as a linear combination of...

please explain step by step 7. Let V be an ndimensional vector space. Suppose S = {v13 - -- ,vk} is a subset of V containing k vectors With k

Robin was assessed for a mild cognitive disability. At her conference, her parents argued that their rights were violated as they were not given the evaluation results prior to the conference, and...

Alkyl halides add to alkenes in the presence of AlCl3; yields are the highest when tertiary halides are used. Predict the outcome of the reaction of tert-pentyl chloride (1-chloro-2,...

and practice using BioSig - ID ? T M here. Question 2 4 2 pts Which of the following statements is CORRECT? Since receivables and payables both result from sales transactions, a firm with a high...

A company issues 1,050 shares of its common stock for $33,600 cash. Prepare journal entries to record this event under each of the following separate situations.