Question: we know that (Z; *) is a group, where ry:=x - 3+ y for all x, y Z. Let y: Z Z be defined

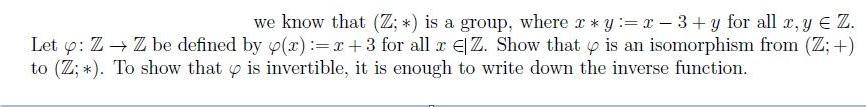
we know that (Z; *) is a group, where ry:=x - 3+

we know that (Z; *) is a group, where ry:=x - 3+ y for all x, y Z. Let y: Z Z be defined by p(x):=x+3 for all x E|Z. Show that is an isomorphism from (Z; +) 4 to (Z; *). To show that is invertible, it is enough to write down the inverse function.

Step by Step Solution

★★★★★

3.35 Rating (142 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The inverse function is defined by xy y 3 for all y EZ Indeed for all x y EZ we ha... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Let L: P1 P2 be defined by L(p(t)) = tp(t) + p(0). Consider the ordered bases S = [t, 1} and S' - {t + 1, t - 1} for P1, and T = [t2, t, 1} and T' = {t2 + 1, t - 1, t + 1} for P2. Find the...

Write down the inverse of each of the following elementary matrices: (a) (b) (c) (d) (e) (f) 1 0 0-0 0001 0010 0160 1000 1000 0010 0-00 0001

Given that z is a standard normal random variable, find z for each situation. a. The area to the left of z is .9750. b. The area between 0 and z is .4750. c. The area to the left of z is .7291. d....

Consider the following version of the lemons problem. There is a continuum of buyers and sellers in the market; the total mass of each group is 1. Each seller has one car to sell and each buyer...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Q4. The CauchySchwcrz Inequality says that if a = (cl....,on} and b 2 (b1... . ,bn) are two vectors in R\". then la'bl S llallllbll- This inequality has many practical applications. In this exercise...

Show that the mapping b(a + bi) = a - bi is an automorphism of the group of complex numbers under addition. Show that b pre- serves complex multiplication as well-that is, b(xy) = b(x)$(v) for all x...

In the population, political party affiliation is 30% Republican, 55% Democratic, and 15% other. To determine whether this distribution is also found among the elderly, in a sample of 100 senior...

If X and Y are independent random variables having failure rate functions x (t ) and y(t ), show that the failure rate function of Z = min(X , Y ) is z (t ) = x (t ) + y(t )

In 2007, nearly 24 million tons of steel mill products went to construction and contracting companies. Transco Steel, a hypothetical manufacturer specializing in the production of steel for this...

Excel application. Consider the following data from BNF Corporation's statement of cash flows for the quarter ended 31 March 2014: Cash received from issuance of capital stock $ 9,499 Cash received...

Find 1 x 2 - 8 x 4 1 2 d x

Match the following terms to the appropriate statement. Some terms may be used more than once and some terms may not be used at all. E-commerce ............. Just-in-time management (JIT) Enterprise...

Match the following terms to the appropriate statement. Some terms may be used more than once and some terms may not be used at all. Budget ........... Managerial Creditors .......... Managers...

Delores Cooper operates Cooper Garden Designs. Most of her customers pay cash so she uses the direct write-off method to account for uncollectible accounts receivable. On May 3, 2014, she determined...

The Institute of Management Accountants Statement of Ethical Professional Practice requires managerial accountants to meet standards regarding the following: Competence Confidentiality Integrity ...

The Hand-to-Mouth Company needs a $10,000 loan for the next 30 days. It is trying to decide which of three alternatives to use: Alternative A: Forgo the discount on its trade credit agreement that...

can i have the answer please? Susan has the newest iPhone, iPad, iPod, and Mac. When a new Apple product is released, Susan stands in line for hours to be the first to buy it. Susan is a(n):...

Show that the complement Ac of the set A of (pointwise) convergence of a sequence of r.v.s {Xn}, n ( 1, is expressed as follows: Ac = {(((; limn( inf Xn(() ( r r,s

Consider the measure space (W, A, ), and define the classes A* and A as follow: A* = {A D M: A A, M N with N A and (N) = 0}, A = {A M: A A, M N with N A and (N) = 0}. Then show that (i) A D M...

By means of an example, show that A j F, j 1, need not imply that j=1 Aj F, and similarly for j=1 Aj.

The Transportation Security Administration (TSA) has examined the possibility of a Registered Traveler program. This program is intended to be a way to shorten security lines for trusted travelers....

The per capita consumption of chicken has risen from 28 pounds in 1960 to 90.6 pounds in 2007, according to the U.S. Department of Agriculture. That constitutes an average increase of approximately...

What sample size is needed to estimate a population mean within 50 of the true mean value using a confidence level of 95%, if the true population variance is known to be 122,500?