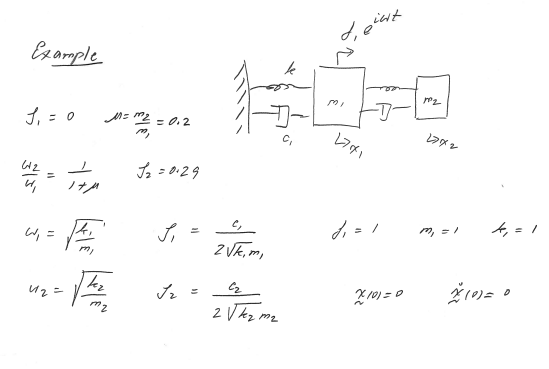
we need to solve this system using complex method approach for a $2$ DOF system

Given $-$ m$1=1,$ k$1=1,$ f$1=1,$ zeta $1=0,$ zeta $2=0\mathrm{.}29$ mu $=$ m$2/$m$1=0\mathrm{.}2$ w$2/$w$1=1/(1+$ mu$)$ w$1=$ sqrt$($k$1/$m$1),$ w$2=$ sqrt$($k$2/$m$2)$ zeta $1=$ c$1/(2*$ sqrt$($k$1*$ m$1)),$ zeta $2=$ c$2/(2*$ sqrt$($k$2*$ m$2))$

Initial condition $$ x$(0)=0,$ x dot $(0)=0$

Step $1-$ find values of m$2,$ c$2,$ k$2,$ w$1$ and w$2$

step $2-$ construct matrix $[$m$],[$c$],[$k$]$ which are $2$x$2$ matrix $[$m$]=[$m$1,0$; $0,$ m$2][$c$]=[$c$1+$ c$2,-$c$2$; $-$c$2,$ c$2+$ c$3][$k$]=[$k$1+$ k$2,-$k$2$; $-$k$2,$ k$2+$ k$3]$ c$3=0,$ k$3=0$

step $3-$ construct $[$Z$($s$)]=($s$^2)*[$m$]+$ s $*[$c$]+[$k$]$

step $4-$ frequency equation $-|$Z$($s$)|=0$ to find $4$ values of s

step $5-$ for each sj$,$ compute rj $=-($Z$11($sj$))/($Z$12($sj$))$ for j $=1,2,3,4$

step $6-$ compute steady state amplitude $-$ a $=([$Z$($iw$)]^-1)*$ f

Step $7-$ compute the coefficient matrix of order $4$x$4$ based on initial condition $[$coeff$]*$ lamda $=$ b lamda $=([$coeff$]^-1)*$ b

step $8-$ compute the total response xk $($t$),$ xk dot $($t$),$ xk double dot $($t$)$ for k $=1,2$ which is the the no$.$ of degree of freedom