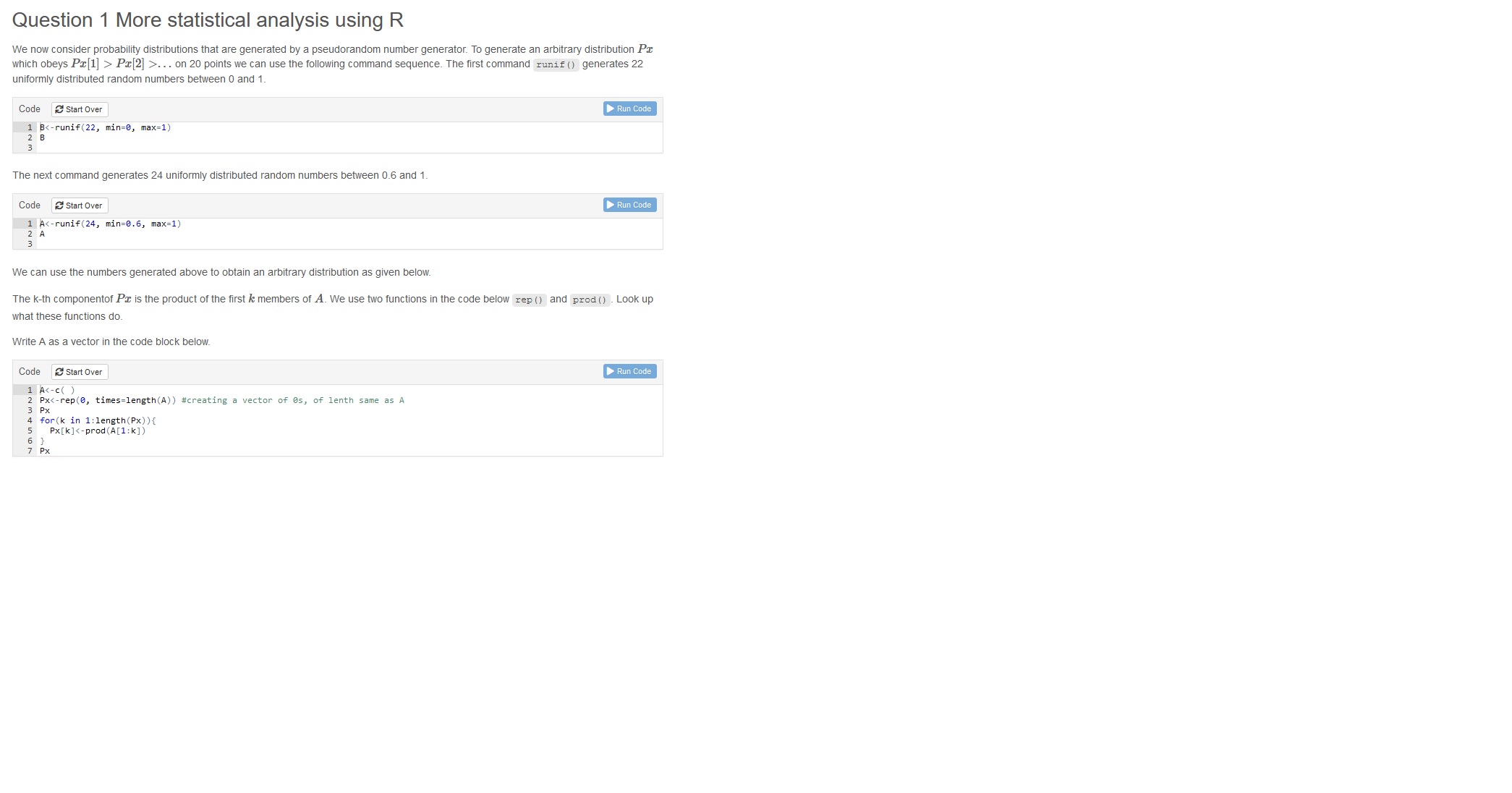
We now consider probability distributions that are generated by a pseudorandom number generator.

To generate an arbitrary distribution Px which obeys Px[1]>Px[2]>... on 20 points

we can use the following command sequence. The first command runif() generates 22 uniformly

distributed random numbers between 0 and 1.

Code

B

B

The next command generates 24 uniformly distributed random numbers between 0.6 and 1.

Code

A

A

We can use the numbers generated above to obtain an arbitrary distribution as given below.

The k-th componentof Px

is the product of the first k members of A

We use two functions in the code below rep() and prod(). Look up what these functions do.

Write as a vector in the code block below.

Code

A

Px

Px

for(k in 1:length(Px)){

Px[k]

}

Px

Question 1 (a) This is not yet a probability distribution. Why not?

What do we need to do to Px to make it a probability distribution? (Hint: Use the comments in the code chunk below to guide you)

Code Space

#Write the code to convert P(X) into a probability distribution

# Write command to find the sum of all the entries in Px

# Write command to rescale Px so that the sum of all the entries in Px is 1

#observe the sum of all entries of Px now and check that it adds to 1.

Write the new vector P(X) in a form that can be used in R code.

Let us call it Px. This vector will be used in the rest of this tutorial

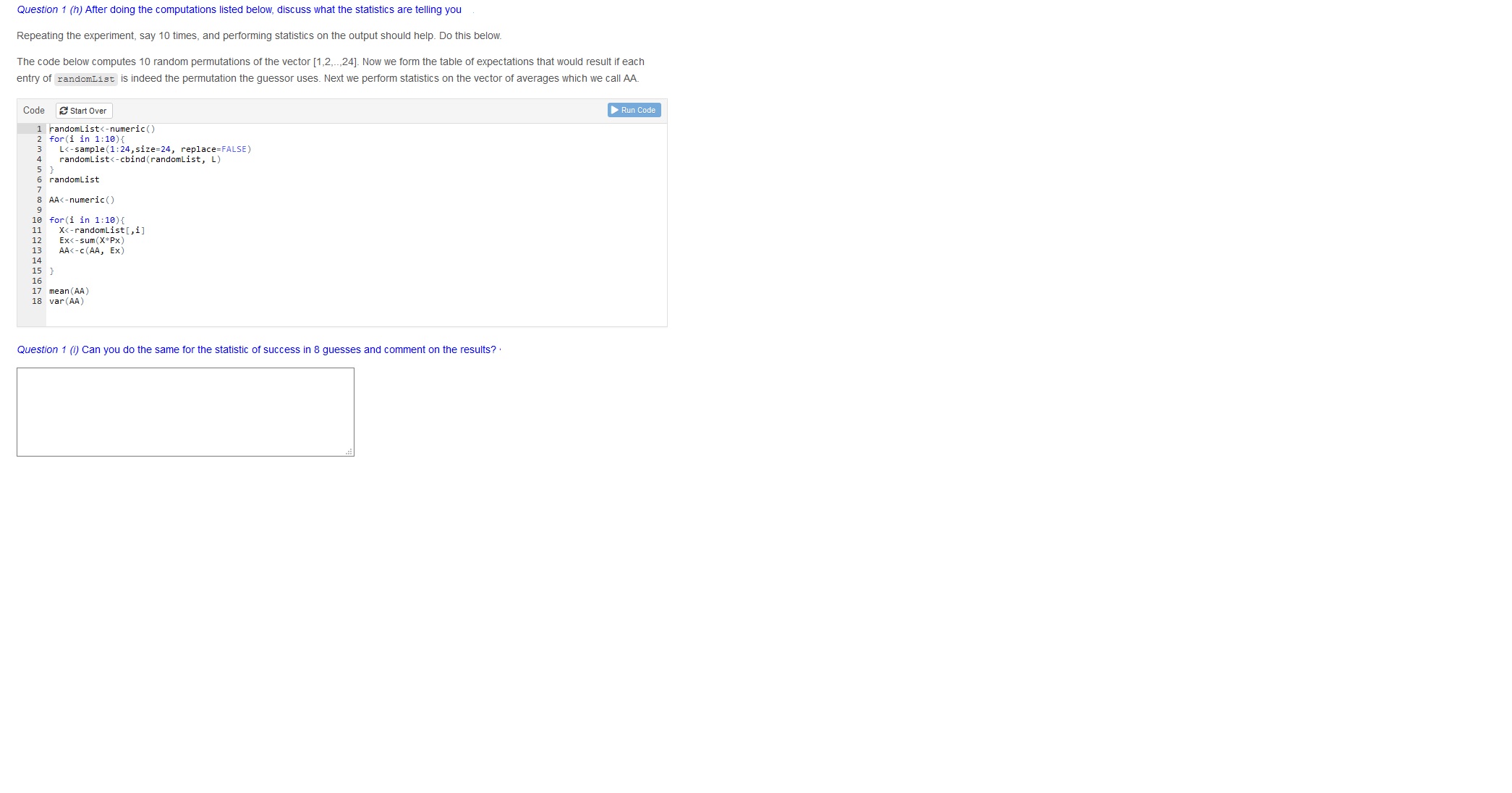
Question 1 (b) Compute the quantities E(X) and Var(X) as well as the square root of Var(X) which is the standard deviation of X. Write code to display the values of E(X), Varx(X) and the standard deviation SD(X).

Question 1(c) Let X be the number of guesses before discovering the secret key and let Px be its probability distribution.

For Px as above, the expected number of guesses before an attacker, who makes the optimal series of guesses, uncovers X is quite low - what is expected number of guesses?.

What would be the expected number of guesses if X was uniformly distributed?

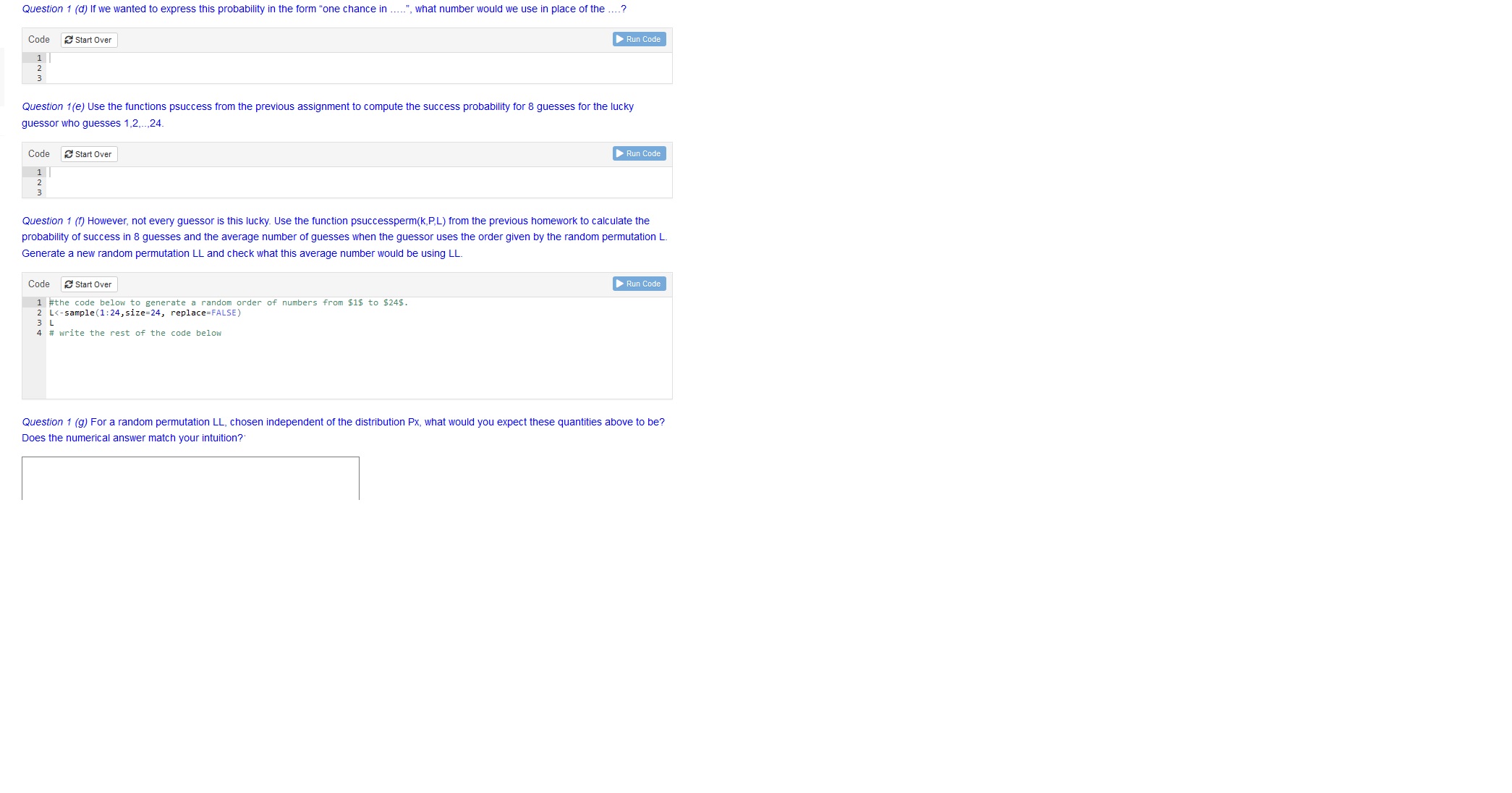
Question 1 (d) If we wanted to express this probability in the form "one chance in .....", what number would we use in place of the ....?

Can yo write code for that ?

Code Space

Question 1 More statistical analysis using R We now consider probability distributions that are generated by a pseudorandom number generator. To generate an arbitrary distribution Pr which obeys Pr[1] > Px 2] >... on 20 points we can use the following command sequence. The first command runif () generates 22 uniformly distributed random numbers between 0 and 1. Code Start Over Run Code WNK 1 B