We often use a loop invariant to prove that an algorithm gives the correct answer. To use a loop invariant to prove correctness, we must show three things about it:

1)Initialization: It is true prior to the first iteration of the loop.

2)Maintenance: If it is true before an iteration of the loop, it remains true before the next iteration.

3)Termination: When the loop terminates, the invariant (usually along with the reason that the loop terminated) gives us a useful property that helps show that the algorithm is correct. Lets take a look at the following Bubble sort algorithm.

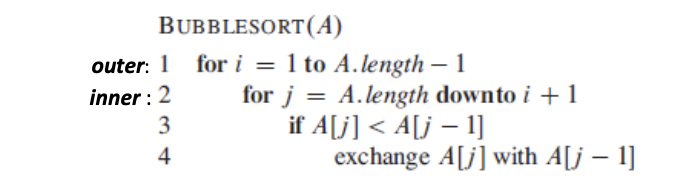Bubble sort is a sorting algorithm that works by repeatedly exchanging adjacent elements that are out of order. Let A denote the output of BUBBLESORT(A). To prove that BUBBLESORT is correct, we need to prove that it terminates and that A[1] A[2] A[n], where n = A.length. In order to show that BUBBLESORT actually sorts, what else do we need to prove?

2) State precisely a loop invariant for the for loop inner, and prove that this loop invariant holds using the above-mentioned structure of the loop invariant.

3) Using the termination condition of the loop invariant proved in part 2), state a loop invariant for the for loop outer that will allow you to prove A[1] A[2] A[n], where n = A.length. Prove that this loop invariant holds using the above-mentioned structure of the loop invariant. You must show/explain your work. Simply stating the answers will result in 0 points awarded. (5 points for #2), 5 points for each of the three parts (Initialization, Maintenance, and Termination) in #3). 20 points in total.)

BUBBLESORT(A) outer: 1 for i = 1 to A.length 1 inner: 2 for j = A.length downto i +1 3 if A[j]