Question: We shall consider the function h given by h(n)=lg(n!) (for n>1). That is, (1) TL h(n)=lg(i)= =lg( lg(i) i=1 i=1 Prove, from the definition

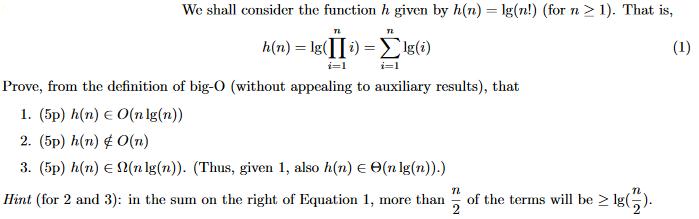
We shall consider the function h given by h(n)=lg(n!) (for n>1). That is, (1) TL h(n)=lg(i)= =lg( lg(i) i=1 i=1 Prove, from the definition of big-O (without appealing to auxiliary results), that 1. (5p) h(n) O(ng(n)) 2. (5p) h(n) 3. (5p) h(n) O(n) (n lg(n)). (Thus, given 1, also h(n) (n Ig(n)).) 72 Hint (for 2 and 3): in the sum on the right of Equation 1, more than of the terms will be > Ig().

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The image youve provided contains a question from a mathematical or computer science context regarding BigO notation which is used to classify algorit... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

c. What is the degree of operating leverage at 17,000 bags and at 22,000 bags? Note: Round your answers to 2 decimal places. Bags 17,000 22,000 Degree of Operating Leverage d. If United Snack Company...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

(1) Question 3. (15 points. We shall consider the function h given by h(n) = 1g(n!) (for n > 1). That is, h(n) = \sc[= 1500 Prove, from the definition of big-O (without appealing to auxiliary...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Submitted to Management Science manuscript MS-0001-1922.65 Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes the journal title....

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

Please help me with the attached article review. I have attached the instructions as well as the scholarly article to use. The topic is Time Value of Money Analysis. Time value of money analysis...

"Fortran, Algol and Lisp invented most programming language concepts 50 years ago; adding the concept of object-orientation suffices to explain all programming languages to date". To what extent is...

Consider an investor who, on January 1, 2016, purchases a TIPS bond with an original principal of $ 100,000, an 8 percent annual (or 4 percent semiannual) coupon rate, and 10 years to maturity. a. If...

Average personal income in one state increased approximately linearly from $23.7 thousand in 2000 to $37.2 thousand in 2010. Average personal income in another state increased approximately linearly...

Depending o n gamma function, the evaluation o f the integral ( 0 e - 2 x x 3 d x )

Enders, Inc., a domestic corporation that invests in foreign securities, reports total taxable income for the tax year of $290,000, consisting of $208,800 in U.S.-source business profits and $81,200...

Shonda receives dividend income from the following foreign and domestic corporations in the current tax year. Determine the amount of U.S.-sourced income for each corporation. Corporation Silver...

Draft a short speech that you will give to your university's Business Club. The title of your talk is "What Is Worldwide Taxation and How Can I Avoid It?"

"U.S. persons are taxed on their worldwide income." Explain.

Liang, a U.S. citizen, owns 100% of ForCo, a foreign corporation not engaged in a U.S. trade or business. Is Liang subject to any U.S. income tax on her dealings with ForCo? Explain.

Question 201 ptA potential client (55-yr-old female) would like to begin an exercise training program. The client questioned if she was fit for exercise. She made concerns of potential limitations...

A reversible liquid-phase isomerization A B is carried out isothermally in a 1000-gal CSTR. The reaction is second order in both the forward and reverse directions. The liquid enters at the top of...

In 1981, the U.S. government put forth the following plan for automobile manufacturers to reduce emissions from automobiles over the next few years. All values are in grams per mile. An automobile...

View the CSB video to list two things in which dust explosions are different from those involving flammable liquids.

Consider the data in Exercise 10 from Chapter 14 and the regression equation to predict commissions earned. a. Plot the residuals in the order in which the data are presented. b. Test for...

Listed below is the selling price for a share of PepsiCo Inc. at the close of each year from 1990 to 2012. .:. a. Plot the data. b. Determine the least squares trend equation. c. Calculate the...

If plotted, the following sales series would appear curvilinear. This indicates that sales are increasing at a somewhat constant annual rate (percent). To fit the sales, therefore, a logarithmic...