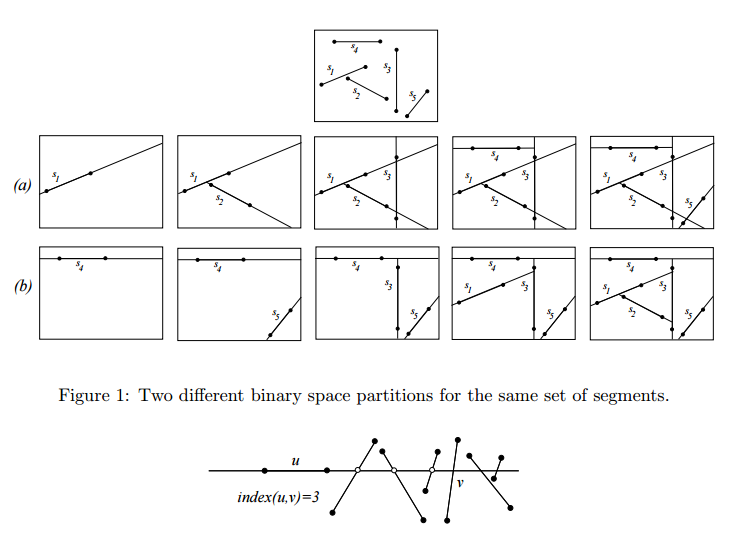
We studied a randomized incremental algorithm for constructing the trapezoidal decomposition. Recall that the geometric structure of the final trapezoidal decomposition is always the same, regardless of the order in which the segments are inserted. However, there are instances of probabilistic constructions in which the final geometric structure depends on the particular order in which the objects are inserted. In this question, you will study one such structure called the Binary Space Partition (BSP). You are given a set of n non intersecting line segments in the plane, and you build a subdivision recursively as follows: Initially, the subdivision contains no segments and only one face, the entire space. When the first segment is inserted, this face is partitioned into two faces by a splitting line that contains this segment. In general, as each segment is added, every face of the existing subdivision that intersects this segment is split by the line containing the segment. An example is shown in Figure 1. In (a), the order of insertion is s₁, s₂, s₃, s₄, s₅. In (b), the order of insertion is s₄, s₅, s₃, s₁, s₂. Observe that different orders of insertions of the segments result in different subdivisions. When a splitting line is added, each future segment which intersects this splitting line is said to be cut by the line. (Therefore, if we say that a segment v is cut by a splitting line containing u, then v must have been inserted after u.) In Figure 1(a), segment s₃ is cut by the line extending segment s₁, and segments s₃ and s₅ are cut by the line extending s₂. Note that segment s₁ is not considered to be cut by s₂ (because s₂ was inserted after s₁).

1. Given n segments in general position, prove that the number of faces of the final BSP subdivision is equal to n + 1 plus the total number of cuts (verify this in the figure above). Hint: Use induction. 2. Give an example of a set of n nonintersecting line segments such that for one insertion order, the resulting BSP has size O(n) and for another insertion order, the BSP has size ?(n ² )

3. Given two line segments u and v, define index(u, v) as follows: If the line containing u does not intersect v, then index(u, v) = ?. Otherwise, define the index to be the number of line segments that intersect this line and lie between v and the closest endpoint of u. (In the figure below, index(u, v) = 3. In Figure 1(a), index(s₂, s₅) = 1, and index(s₁, s₃) = 0.) Prove that if the segments are inserted in random order, then the probability that u cuts v is at most 1 / index(u,v)+2 .

4. Assuming that segments are inserted in random order, use the results of parts (a) and (c) to prove that the expected number of faces in the subdivision is O(n log n). Hint: You need to show that the expected total number of cuts is O(n log n). To show this, you should first find the expected number of segments that the i-th segment (i.e., i-th in the random order) cuts.

Please write the algorithm, a justification of its correctness, and a derivation of its running time. Write clear and convincing PSEUDO-CODE for your algorithm. NO CODE.