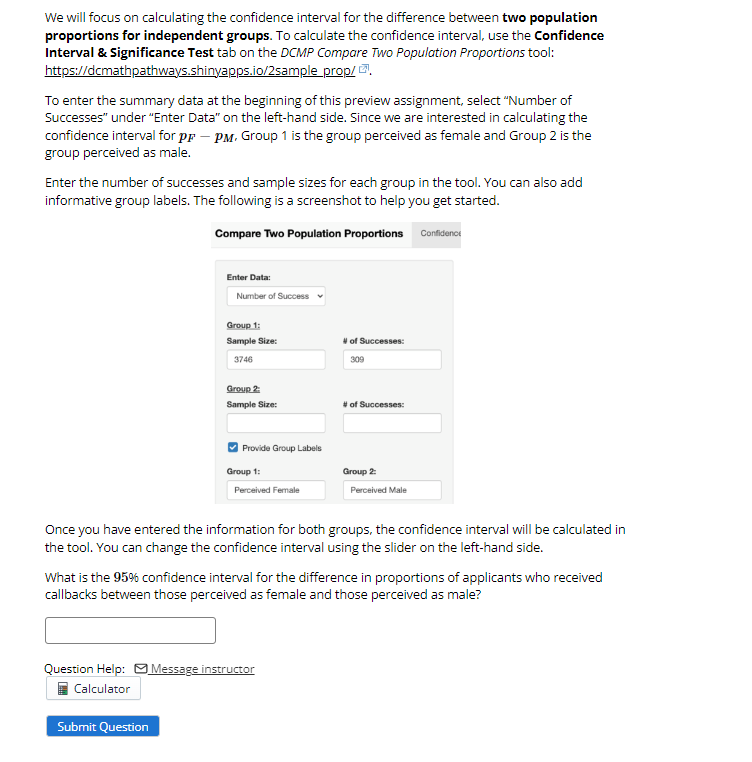
We will focus on calculating the confidence interval for the difference between two population proportions for independent groups. To calculate the confidence interval, use the Confidence Interval & Significance Test tab on the DCMP Compare Two Population Proportions tool: https://dcmathpathways.shinyapps.io/2sample_prop/ c. To enter the summary data at the beginning of this preview assignment, select "Number of Successes" under "Enter Data" on the left-hand side. Since we are interested in calculating the confidence interval for pp - PM, Group 1 is the group perceived as female and Group 2 is the group perceived as male. Enter the number of successes and sample sizes for each group in the tool. You can also add informative group labels. The following is a screenshot to help you get started. Compare Two Population Proportions Confidence Enter Data: Number of Success Group 1: Sample Size: # of Successes: 3746 309 Group 2 Sample Size: # of Successes: Provide Group Labels Group 1: Group 2: Perceived Fernale Perceived Male Once you have entered the information for both groups, the confidence interval will be calculated in the tool. You can change the confidence interval using the slider on the left-hand side. What is the 959% confidence interval for the difference in proportions of applicants who received callbacks between those perceived as female and those perceived as male? Question Help: ( Message instructor Calculator Submit